已知:
一、第一種飲料是咖啡或啤酒。
二、第二種飲料不是汽水,第三種飲料不是可樂。
三、第四種飲料是可樂或啤酒。
四、第三或第四種飲料是啤酒。
請問,咖啡、汽水、可樂、啤酒各是第幾種飲料?
謎題1:咖啡、可樂、汽水、啤酒
謎題2:三個盒子
有三個盒子,一只金的、一只銀的、一只是鉛的,其中一個有一個肖像。每只盒子上寫有一句:
金盒:肖像在這盒子;
銀盒:肖像不在這盒中;
鉛盒:肖像不在金盒中。
已知以上三句中,只有一句是真。問肖像放在那個盒中?
謎題2:鉛盒字條為真 肖像在銀盒
謎題3:四少女的姓名
敏敏、慧慧、芳芳、文文都是四個好朋友。文文從北京回來,其他三人來她家看望。
芳芳說:“小劉考上大學。”
小劉說:“這要多謝慧慧、是她幫忙。”
小金說:“慧慧固然有功,但主要還是靠你的實力。”
這時郵差送來一封信:“吳小姐,你的信。”
芳芳說:“快看你爸爸寄來的信,我先和小林談一談。”
問:你可知她們的姓名? 謎題3:吳文文 劉敏敏 林慧慧 金芳芳
謎題4:丁勝了幾場?
甲、乙、丙、丁四人比賽乒乓球,每兩個人都要賽一場。結果甲勝了丁,並且甲、乙、丙三人勝的場數相同,問丁勝了幾場?
謎題4:0場 (2012-8-15修改)
謎題5:弗里曼先生的未婚妻
弗里曼先生認識埃達、比、茜德、黛布、伊芙這五位女士。
.(一) 五位女士分為兩個年齡類別:三位女士小於 30 歲,兩位女士大於 30 歲。
.(二) 兩位女士是教師,其他三位女士是秘書。
.(三) 埃達和茜德屬於相同的年齡類別。
.(四) 黛布和伊芙屬於不同的年齡類別。
.(五) 比和伊芙的職業相同。
.(六) 茜德和黛布的職業不同。
.(七) 弗里曼先生將同其中一位年齡大於 30 歲的教師結婚。
誰是弗里曼先生的未婚妻?
謎題5:黛布
謎題2:三個盒子
有三個盒子,一只金的、一只銀的、一只是鉛的,其中一個有一個肖像。每只盒子上寫有一句:
金盒:肖像在這盒子;
銀盒:肖像不在這盒中;
鉛盒:肖像不在金盒中。
已知以上三句中,只有一句是真。問肖像放在那個盒中?
謎題2:鉛盒字條為真 肖像在銀盒
謎題3:四少女的姓名
敏敏、慧慧、芳芳、文文都是四個好朋友。文文從北京回來,其他三人來她家看望。
芳芳說:“小劉考上大學。”
小劉說:“這要多謝慧慧、是她幫忙。”
小金說:“慧慧固然有功,但主要還是靠你的實力。”
這時郵差送來一封信:“吳小姐,你的信。”
芳芳說:“快看你爸爸寄來的信,我先和小林談一談。”
問:你可知她們的姓名? 謎題3:吳文文 劉敏敏 林慧慧 金芳芳
謎題4:丁勝了幾場?
甲、乙、丙、丁四人比賽乒乓球,每兩個人都要賽一場。結果甲勝了丁,並且甲、乙、丙三人勝的場數相同,問丁勝了幾場?
謎題4:0場 (2012-8-15修改)
謎題5:弗里曼先生的未婚妻
弗里曼先生認識埃達、比、茜德、黛布、伊芙這五位女士。
.(一) 五位女士分為兩個年齡類別:三位女士小於 30 歲,兩位女士大於 30 歲。
.(二) 兩位女士是教師,其他三位女士是秘書。
.(三) 埃達和茜德屬於相同的年齡類別。
.(四) 黛布和伊芙屬於不同的年齡類別。
.(五) 比和伊芙的職業相同。
.(六) 茜德和黛布的職業不同。
.(七) 弗里曼先生將同其中一位年齡大於 30 歲的教師結婚。
誰是弗里曼先生的未婚妻?
謎題5:黛布
【1】假設有一個池塘,裡面有無窮多的水。現有2個空水壺,容積分別為5升和6升。問題是如何只用這2個水壺從池塘裡取得3升的水。
A:由滿6向空5倒,剩1升,把這1升倒5裡,然後6剩滿,倒5裡面,由於5裡面有1升水,因此6只能向5倒4升水,然後將6剩餘的2升,倒入空的5裡面,再灌滿6向5裡倒3升,剩餘3升。
【2】周雯的媽媽是豫林水泥廠的化驗員。一天,周雯來到化驗室做作業。做完後想出去玩。"等等,媽媽還要考你一個題目,"她接著說,"你看這6只做化驗用的玻璃杯,前面3只盛滿了水,後面3只是空的。你能只移動1只玻璃杯,就便盛滿水的杯子和空杯子間隔起來嗎?"愛動腦筋的周雯,是學校裡有名的"小機靈",她只想了一會兒就做到了。請你想想看,"小機靈"是怎樣做的?
A:設杯子編號為ABCDEF,ABC為滿,DEF為空,把B中的水倒進E中即可。
【3】三個小夥子同時愛上了一個姑娘,為了決定他們誰能娶這個姑娘,他們決定用手槍進行一次決鬥。小李的命中率是30%,小黃比他好些,命中率是50%,最出色的槍手是小林,他從不失誤,命中率是100%。由於這個顯而易見的事實,為公平起見,他們決定按這樣的順序:小李先開槍,小黃第二,小林最後。然後這樣迴圈,直到他們只剩下一個人。
那麼這三個人中誰活下來的機會最大呢?他們都應該採取什麼樣的策略?
A: 小林在輪到自己且小黃沒死的條件下必殺黃,再跟菜鳥李單挑。
所以黃在林沒死的情況下必打林,否則自己必死。
小李經過計算比較(過程略),會決定自己先打小林。
於是經計算,小李有873/2600≈33.6%的生機;
小黃有109/260≈41.9%的生機;
小林有24.5%的生機。
哦,這樣,那小李的第一槍會朝天開,以後當然是打敵人,誰活著打誰;
小黃一如既往先打林,小林還是先幹掉黃,冤家路窄啊!
最後李,黃,林存活率約38:27:35;
菜鳥活下來抱得美人歸的機率大。
李先放一空槍(如果合夥幹中林,自己最吃虧)黃會選林打一槍(如不打林,自己肯定先玩完了)林會選黃打一槍(畢竟它命中率高)李黃對決0.3:0.280.4可能性李林對決0.3:0.60.6可能性成功率0.73
李和黃打林李黃對決0.3:0.40.7*0.4可能性李林對決0.3:0.7*0.6*0.70.7*0.6可能性成功率0.64
【4】一間囚房裡關押著兩個犯人。每天監獄都會為這間囚房提供一罐湯,讓這兩個犯人自己來分。起初,這兩個人經常會發生爭執,因為他們總是有人認為對方的湯比自己的多。後來他們找到了一個兩全其美的辦法:一個人分湯,讓另一個人先選。於是爭端就這麼解決了。
可是,現在這間囚房裡又加進來一個新犯人,現在是三個人來分湯。必須尋找一個新的方法來維持他們之間的和平。該怎麼辦呢?按:心理問題,不是邏輯問題
A:是讓甲分湯,分好後由乙和丙按任意順序給自己挑湯,剩餘一碗留給甲。這樣乙和丙兩人的總和肯定是他們兩人可拿到的最大。然後將他們兩人的湯混合之後再按兩人的方法再次分湯。
【5】在一張長方形的桌面上放了n個一樣大小的圓形硬幣。這些硬幣中可能有一些不完全在桌面內,也可能有一些彼此重疊;當再多放一個硬幣而它的圓心在桌面內時,新放的硬幣便必定與原先某些硬幣重疊。
A: 小林在輪到自己且小黃沒死的條件下必殺黃,再跟菜鳥李單挑。
所以黃在林沒死的情況下必打林,否則自己必死。
小李經過計算比較(過程略),會決定自己先打小林。
於是經計算,小李有873/2600≈33.6%的生機;
小黃有109/260≈41.9%的生機;
小林有24.5%的生機。
哦,這樣,那小李的第一槍會朝天開,以後當然是打敵人,誰活著打誰;
小黃一如既往先打林,小林還是先幹掉黃,冤家路窄啊!
最後李,黃,林存活率約38:27:35;
菜鳥活下來抱得美人歸的機率大。
李先放一空槍(如果合夥幹中林,自己最吃虧)黃會選林打一槍(如不打林,自己肯定先玩完了)林會選黃打一槍(畢竟它命中率高)李黃對決0.3:0.280.4可能性李林對決0.3:0.60.6可能性成功率0.73
李和黃打林李黃對決0.3:0.40.7*0.4可能性李林對決0.3:0.7*0.6*0.70.7*0.6可能性成功率0.64
【4】一間囚房裡關押著兩個犯人。每天監獄都會為這間囚房提供一罐湯,讓這兩個犯人自己來分。起初,這兩個人經常會發生爭執,因為他們總是有人認為對方的湯比自己的多。後來他們找到了一個兩全其美的辦法:一個人分湯,讓另一個人先選。於是爭端就這麼解決了。
可是,現在這間囚房裡又加進來一個新犯人,現在是三個人來分湯。必須尋找一個新的方法來維持他們之間的和平。該怎麼辦呢?按:心理問題,不是邏輯問題
A:是讓甲分湯,分好後由乙和丙按任意順序給自己挑湯,剩餘一碗留給甲。這樣乙和丙兩人的總和肯定是他們兩人可拿到的最大。然後將他們兩人的湯混合之後再按兩人的方法再次分湯。
【5】在一張長方形的桌面上放了n個一樣大小的圓形硬幣。這些硬幣中可能有一些不完全在桌面內,也可能有一些彼此重疊;當再多放一個硬幣而它的圓心在桌面內時,新放的硬幣便必定與原先某些硬幣重疊。
請證明整個桌面可以用4n個硬幣完全覆蓋。
A:要想讓新放的硬幣不與原先的硬幣重疊,兩個硬幣的圓心距必須大於直徑。也就是說,對於桌面上任意一點,到最近的圓心的距離都小於2,所以,整個桌面可以用n個半徑為2的硬幣覆蓋。
把桌面和硬幣的尺度都縮小一倍,那麼,長、寬各是原桌面一半的小桌面,就可以用n個半徑為1的硬幣覆蓋。那麼,把原來的桌子分割成相等的4塊小桌子,那麼每塊小桌子都可以用n個半徑為1的硬幣覆蓋,因此,整個桌面就可以用4n個半徑為1的硬幣覆蓋。
【6】一個球、一把長度大約是球的直徑2/3長度的直尺.你怎樣測出球的半徑?方法很多,看看誰的比較巧妙
A:要想讓新放的硬幣不與原先的硬幣重疊,兩個硬幣的圓心距必須大於直徑。也就是說,對於桌面上任意一點,到最近的圓心的距離都小於2,所以,整個桌面可以用n個半徑為2的硬幣覆蓋。
把桌面和硬幣的尺度都縮小一倍,那麼,長、寬各是原桌面一半的小桌面,就可以用n個半徑為1的硬幣覆蓋。那麼,把原來的桌子分割成相等的4塊小桌子,那麼每塊小桌子都可以用n個半徑為1的硬幣覆蓋,因此,整個桌面就可以用4n個半徑為1的硬幣覆蓋。
【6】一個球、一把長度大約是球的直徑2/3長度的直尺.你怎樣測出球的半徑?方法很多,看看誰的比較巧妙
A:把球平放在平整的台面上,把直尺垂直于台面并使尺的刻线相切于球面,其切点的高度就是球的半径,因直尺的长度大于直径的2/3,也就是说大于球的半径,所以能测量。
【7】五個大小相同的一元人民幣硬幣。要求兩兩相接觸,應該怎麼擺?A:底下放一個1,然後2 3放在1上面,另外的4 5豎起來放在1的上面。
【8】猜牌問題S先生、P先生、Q先生他們知道桌子的抽屜裡有16張撲克牌:紅桃A、Q、4黑桃J、8、4、2、7、3草花K、Q、5、4、6方塊A、5。約翰教授從這16張牌中挑出一張牌來,並把這張牌的點數告訴P先生,把這張牌的花色告訴Q先生。這時,約翰教授問P先生和Q先生:你們能從已知的點數或花色中推知這張牌是什麼牌嗎?於是,S先生聽到如下的對話:P先生:我不知道這張牌。Q先生:我知道你不知道這張牌。P先生:現在我知道這張牌了。Q先生:我也知道了。聽罷以上的對話,S先生想了一想之後,就正確地推出這張牌是什麼牌。請問:這張牌是什麼牌?
【7】五個大小相同的一元人民幣硬幣。要求兩兩相接觸,應該怎麼擺?A:底下放一個1,然後2 3放在1上面,另外的4 5豎起來放在1的上面。
【8】猜牌問題S先生、P先生、Q先生他們知道桌子的抽屜裡有16張撲克牌:紅桃A、Q、4黑桃J、8、4、2、7、3草花K、Q、5、4、6方塊A、5。約翰教授從這16張牌中挑出一張牌來,並把這張牌的點數告訴P先生,把這張牌的花色告訴Q先生。這時,約翰教授問P先生和Q先生:你們能從已知的點數或花色中推知這張牌是什麼牌嗎?於是,S先生聽到如下的對話:P先生:我不知道這張牌。Q先生:我知道你不知道這張牌。P先生:現在我知道這張牌了。Q先生:我也知道了。聽罷以上的對話,S先生想了一想之後,就正確地推出這張牌是什麼牌。請問:這張牌是什麼牌?
A:方塊5
【9】一個教授邏輯學的教授,有三個學生,而且三個學生均非常聰明!一天教授給他們出了一個題,教授在每個人腦門上貼了一張紙條並告訴他們,每個人的紙條上都寫了一個正整數,且某兩個數的和等於第三個!(每個人可以看見另兩個數,但看不見自己的)教授問第一個學生:你能猜出自己的數嗎?回答:不能,問第二個,不能,第三個,不能,再問第一個,不能,第二個,不能,第三個:我猜出來了,是144!
【9】一個教授邏輯學的教授,有三個學生,而且三個學生均非常聰明!一天教授給他們出了一個題,教授在每個人腦門上貼了一張紙條並告訴他們,每個人的紙條上都寫了一個正整數,且某兩個數的和等於第三個!(每個人可以看見另兩個數,但看不見自己的)教授問第一個學生:你能猜出自己的數嗎?回答:不能,問第二個,不能,第三個,不能,再問第一個,不能,第二個,不能,第三個:我猜出來了,是144!
教授很滿意的笑了。請問您能猜出另外兩個人的數嗎?A:經過第一輪,說明任何兩個數都是不同的。
第二輪,前兩個人沒有猜出,說明任何一個數都不是其它數的兩倍。現在有了以下幾個條件:1.每個數大於02.兩兩不等3.任意一個數不是其他數的兩倍。每個數字可能是另兩個之和或之差,第三個人能猜出144,必然根據前面三個條件排除了其中的一種可能。假設:是兩個數之差,即x-y=144。這時1(x,y>0)和2(x!=y)都滿足,所以要否定x+y必然要使3不滿足,即x+y=2y,解得x=y,不成立(不然第一輪就可猜出),所以不是兩數之差。因此是兩數之和,即x+y=144。同理,這時1,2都滿足,必然要使3不滿足,即x-y=2y,兩方程聯立,可得x=108,y=36。
這兩輪猜的順序其實分別為這樣:
這兩輪猜的順序其實分別為這樣:
第一輪(一號,二號),第二輪(三號,一號,二號)。
這樣分大家在每輪結束時獲得的資訊是相同的(即前面的三個條件)。
那麼就假設我們是C,來看看C是怎麼做出來的:C看到的是A的36和B的108,因為條件,兩個數的和是第三個,那麼自己要麼是72要麼是144(猜到這個是因為72的話,108就是36和72的和,144的話就是108和36的和。這樣子這句話看不懂的舉手):
假設自己(C)是72的話,那麼B在第二回合的時候就可以看出來,下面是如果C是72,B的思路:這種情況下,B看到的就是A的36和C的72,那麼他就可以猜自己,是36或者是108(猜到這個是因為36的話,36加36等於72,108的話就是36和108的和):
如果假設自己(B)頭上是36,那麼,C在第一回合的時候就可以看出來,下面是如果B是36,C的思路:這種情況下,C看到的就是A的36和B的36,那麼他就可以猜自己,是72或者是0(這個不再解釋了):
如果假設自己(C)頭上是0,那麼,A在第一回合的時候就可以看出來,下面是如果C是0,A的思路:這種情況下,A看到的就是B的36和C的0,那麼他就可以猜自己,是36或者是36(這個不再解釋了),那他可以一口報出自己頭上的36。(然後是逆推逆推逆推),現在A在第一回合沒報出自己的36,C(在B的想象中)就可以知道自己頭上不是0,如果其他和B的想法一樣(指B頭上是36),那麼C在第一回合就可以報出自己的72。現在C在第一回合沒報出自己的36,B(在C的想象中)就可以知道自己頭上不是36,如果其他和C的想法一樣(指C頭上是72),那麼B在第二回合就可以報出自己的108。現在B在第二回合沒報出自己的108,C就可以知道自己頭上不是72,那麼C頭上的唯一可能就是144了。
史上最雷人的應聘者
那麼就假設我們是C,來看看C是怎麼做出來的:C看到的是A的36和B的108,因為條件,兩個數的和是第三個,那麼自己要麼是72要麼是144(猜到這個是因為72的話,108就是36和72的和,144的話就是108和36的和。這樣子這句話看不懂的舉手):
假設自己(C)是72的話,那麼B在第二回合的時候就可以看出來,下面是如果C是72,B的思路:這種情況下,B看到的就是A的36和C的72,那麼他就可以猜自己,是36或者是108(猜到這個是因為36的話,36加36等於72,108的話就是36和108的和):
如果假設自己(B)頭上是36,那麼,C在第一回合的時候就可以看出來,下面是如果B是36,C的思路:這種情況下,C看到的就是A的36和B的36,那麼他就可以猜自己,是72或者是0(這個不再解釋了):
如果假設自己(C)頭上是0,那麼,A在第一回合的時候就可以看出來,下面是如果C是0,A的思路:這種情況下,A看到的就是B的36和C的0,那麼他就可以猜自己,是36或者是36(這個不再解釋了),那他可以一口報出自己頭上的36。(然後是逆推逆推逆推),現在A在第一回合沒報出自己的36,C(在B的想象中)就可以知道自己頭上不是0,如果其他和B的想法一樣(指B頭上是36),那麼C在第一回合就可以報出自己的72。現在C在第一回合沒報出自己的36,B(在C的想象中)就可以知道自己頭上不是36,如果其他和C的想法一樣(指C頭上是72),那麼B在第二回合就可以報出自己的108。現在B在第二回合沒報出自己的108,C就可以知道自己頭上不是72,那麼C頭上的唯一可能就是144了。
史上最雷人的應聘者
【10】某城市發生了一起汽車撞人逃跑事件,該城市只有兩種顏色的車,藍15%綠85%,事發時有一個人在現場看見了,他指證是藍車,但是根據專家在現場分析,當時那種條件能看正確的可能性是80%那麼,肇事的車是藍車的概率到底是多少?A: 15%*80%/(85%×20%+15%*80%)
【11】有一人有240公斤水,他想運往乾旱地區賺錢。他每次最多攜帶60公斤,並且每前進一公里須耗水1公斤(均勻耗水)。假設水的價格在出發地為0,以後,與運輸路程成正比,(即在10公里處為10元/公斤,在20公里處為20元/公斤......),又假設他必須安全返回,請問,他最多可賺多少錢?A: f(x)=(60-2x)*x,當x=15時,有最大值450。
450×4
【12】現在共有100匹馬跟100塊石頭,馬分3種,大型馬;中型馬跟小型馬。其中一匹大馬一次可以馱3塊石頭,中型馬可以馱2塊,而小型馬2頭可以馱一塊石頭。問需要多少匹大馬,中型馬跟小型馬?(問題的關鍵是剛好必須是用完100匹馬)
A:
6種結果
【13】 (陷阱題)
1=5,2=15,3=215,4=2145那麼5=?
A: 因為1=5,所以5=1.
【14】有2n個人排隊進電影院,票價是50美分。在這2n個人當中,其中n個人只有50美分,另外n個人有1美元(紙票子)。愚蠢的電影院開始賣票時1分錢也沒有。問:有多少種排隊方法使得每當一個擁有1美元買票時,電影院都有50美分找錢
注:1美元=100美分擁有1美元的人,擁有的是紙幣,沒法破成2個50美分A:本題可用遞迴演算法,但時間複雜度為2的n次方,也可以用動態規劃法,時間複雜度為n的平方,實現起來相對要簡單得多,但最方便的就是直接運用公式:排隊的種數=(2n)!/[n!(n+1)!]。
如果不考慮電影院能否找錢,那麼一共有(2n)!/[n!n!]種排隊方法(即從2n個人中取出n個人的組合數),對於每一種排隊方法,如果他會導致電影院無法找錢,則稱為不合格的,這種的排隊方法有(2n)!/[(n-1)!(n+1)!](從2n個人中取出n-1個人的組合數)種,所以合格的排隊種數就是(2n)!/[n!n!]- (2n)!/[(n-1)!(n+1)!] =(2n)!/[n!(n+1)!]。至於為什麼不合格數是(2n)!/[(n-1)!(n+1)!],說起來太複雜,這裡就不講了。
【15】一個人花8塊錢買了一隻雞,9塊錢賣掉了,然後他覺得不划算,花10塊錢又買回來了,11塊賣給另外一個人。問他賺了多少?
A:
2元
【16】有一種體育競賽共含M個專案,有運動員A,B,C參加,在每一專案中,第一,第二,第三名分別的X,Y,Z分,其中X,Y,Z為正整數且X>Y>Z。最後A得22分,B與C均得9分,B在百米賽中取得第一。求M的值,並問在跳高中誰得第二名。
A:
因為ABC三人得分共40分,三名得分都為正整數且不等,所以前三名得分最少為6分,40=5*8=4*10=2*2
0=1*20,不難得出專案數只能是5.即M=5.
A得分為22分,共5項,所以每項第一名得分只能是5,故A應得4個一名一個二名.22=5*4+2,第二名得1分,又B百米得第一,所以A只能得這個第二.
B的5項共9分,其中百米第一5分
,其它4項全是1分,9=5+1=1+1+1.即B除百米第一外全是第三,跳高第二必定是C所得.
【17】前提:
1 有五棟五種顏色的房子
2 每一位房子的主人國籍都不同
3 這五個人每人只喝一種飲料,只抽一種牌子的香菸,只養一種寵物
4 沒有人有相同的寵物,抽相同牌子的香菸,喝相同的飲料
提示:
1 英國人住在紅房子裡
2 瑞典人養了一條狗
3 丹麥人喝茶
4 綠房子在白房子左邊
5 綠房子主人喝咖啡
6 抽PALL MALL煙的人養了一隻鳥
7 黃房子主人抽DUNHILL煙
8 住在中間那間房子的人喝牛奶
9 挪威人住第一間房子
10 抽混合煙的人住在養貓人的旁邊
11 養馬人住在抽DUNHILL煙的人旁邊
12 抽BLUE MASTER煙的人喝啤酒
13 德國人抽PRINCE煙
14 挪威人住在藍房子旁邊
2 瑞典人養了一條狗
3 丹麥人喝茶
4 綠房子在白房子左邊
5 綠房子主人喝咖啡
6 抽PALL MALL煙的人養了一隻鳥
7 黃房子主人抽DUNHILL煙
8 住在中間那間房子的人喝牛奶
9 挪威人住第一間房子
10 抽混合煙的人住在養貓人的旁邊
11 養馬人住在抽DUNHILL煙的人旁邊
12 抽BLUE MASTER煙的人喝啤酒
13 德國人抽PRINCE煙
14 挪威人住在藍房子旁邊
15 抽混合煙的人的鄰居喝礦泉水
問題是:誰養魚???
第一間是黃房子,挪威人住,喝礦泉水,抽DUNHILL香菸,養貓;
問題是:誰養魚???
第一間是黃房子,挪威人住,喝礦泉水,抽DUNHILL香菸,養貓;
第二間是藍房子,丹麥人住,喝茶,抽混合煙,養馬;
第三間是紅房子,英國人住,喝牛奶,抽PALL MALL煙,養鳥;
第四間是綠房子,德國人住,喝咖啡,抽PRINCE煙,養貓、馬、鳥、狗以外的寵物;
第五間是白房子,瑞典人住,喝啤酒,抽BLUE MASTER煙,養狗。
【18】5個人來自不同地方,住不同房子,養不同動物,吸不同牌子香菸,喝不同飲料,喜歡不同食物。
根據以下線索確定誰是養貓的人。
1. 紅房子在藍房子的右邊,白房子的左邊(不一定緊鄰)
2. 黃房子的主人來自香港,而且他的房子不在最左邊。
3. 愛吃比薩的人住在愛喝礦泉水的人的隔壁。
4. 來自北京的人愛喝茅臺,住在來自上海的人的隔壁。
5. 吸希爾頓香菸的人住在養馬人的右邊隔壁。
6. 愛喝啤酒的人也愛吃雞。
7. 綠房子的人養狗。
8. 愛吃麵條的人住在養蛇人的隔壁。
9. 來自天津的人的鄰居(緊鄰)一個愛吃牛肉,另一個來自成都。
10.養魚的人住在最右邊的房子裡。
11.吸萬寶路香菸的人住在吸希爾頓香菸的人和吸“555”香菸的人的中間(緊鄰)
12.紅房子的人愛喝茶。
13.愛喝葡萄酒的人住在愛吃豆腐的人的右邊隔壁。
14.吸紅塔山香菸的人既不住在吸健牌香菸的人的隔壁,也不與來自上海的人相鄰。
15.來自上海的人住在左數第二間房子裡。
16.愛喝礦泉水的人住在最中間的房子裡。
17.愛吃麵條的人也愛喝葡萄酒。
18.吸“555”香菸的人比吸希爾頓香菸的人住的靠右
第一間是蘭房子,住北京人,養馬,抽健牌香菸,喝茅臺,吃豆腐;
【18】5個人來自不同地方,住不同房子,養不同動物,吸不同牌子香菸,喝不同飲料,喜歡不同食物。
根據以下線索確定誰是養貓的人。
1. 紅房子在藍房子的右邊,白房子的左邊(不一定緊鄰)
2. 黃房子的主人來自香港,而且他的房子不在最左邊。
3. 愛吃比薩的人住在愛喝礦泉水的人的隔壁。
4. 來自北京的人愛喝茅臺,住在來自上海的人的隔壁。
5. 吸希爾頓香菸的人住在養馬人的右邊隔壁。
6. 愛喝啤酒的人也愛吃雞。
7. 綠房子的人養狗。
8. 愛吃麵條的人住在養蛇人的隔壁。
9. 來自天津的人的鄰居(緊鄰)一個愛吃牛肉,另一個來自成都。
10.養魚的人住在最右邊的房子裡。
11.吸萬寶路香菸的人住在吸希爾頓香菸的人和吸“555”香菸的人的中間(緊鄰)
12.紅房子的人愛喝茶。
13.愛喝葡萄酒的人住在愛吃豆腐的人的右邊隔壁。
14.吸紅塔山香菸的人既不住在吸健牌香菸的人的隔壁,也不與來自上海的人相鄰。
15.來自上海的人住在左數第二間房子裡。
16.愛喝礦泉水的人住在最中間的房子裡。
17.愛吃麵條的人也愛喝葡萄酒。
18.吸“555”香菸的人比吸希爾頓香菸的人住的靠右
第一間是蘭房子,住北京人,養馬,抽健牌香菸,喝茅臺,吃豆腐;
第二間是綠房子,住上海人,養狗,抽希爾頓,喝葡萄酒,吃麵條;
第三間是黃房子,住香港人,養蛇,抽萬寶路,喝礦泉水,吃牛肉;
第四間是紅房子,住天津人,抽555,喝茶,吃比薩;
第五間是白房子,住成都人,養魚,抽紅塔山,喝啤酒,吃雞。
【19】鬥地主附殘局
地主手中牌2、K、Q、J、10、9、8、8、6、6、5、5、3、3、3、3、7、7、7、7
長工甲手中牌大王、小王、2、A、K、Q、J、10、Q、J、10、9、8、5、5、4、4
長工乙手中牌2、2、A、A、A、K、K、Q、J、10、9、9、8、6、6、4、4
三家都是明手,互知底牌。
要求是:在三家都不打錯牌的情況下,地主必須要麼輸要麼贏。問:哪方會贏?
【19】鬥地主附殘局
地主手中牌2、K、Q、J、10、9、8、8、6、6、5、5、3、3、3、3、7、7、7、7
長工甲手中牌大王、小王、2、A、K、Q、J、10、Q、J、10、9、8、5、5、4、4
長工乙手中牌2、2、A、A、A、K、K、Q、J、10、9、9、8、6、6、4、4
三家都是明手,互知底牌。
要求是:在三家都不打錯牌的情況下,地主必須要麼輸要麼贏。問:哪方會贏?
A: 無解地主怎麼出都會輸
【20】 (邊換樓邊比較,大的在手)
一樓到十樓的每層電梯門口都放著一顆鑽石,鑽石大小不一。你乘坐電梯從一樓到十樓,每層樓電梯門都會開啟一次,只能拿一次鑽石,問怎樣才能拿到最大的一顆?
A: 先拿下第一樓的鑽石,然後在每一樓把手中的鑽石與那一樓的鑽石相比較,如果那一樓的鑽石比手中的鑽石大的話那就把手中的鑽石換成那一層的鑽石。
【21】U2合唱團在17分鐘 內得趕到演唱會場,途中必需跨過一座橋,四個人從橋的同一端出發,你得幫助他們到達另一端,天色很暗,而他們只有一隻手電筒。一次同時最多可以有兩人一起 過橋,而過橋的時候必須持有手電筒,所以就得有人把手電筒帶來帶去,來回橋兩端。手電筒是不能用丟的方式來傳遞的。四個人的步行速度各不同,若兩人同行則 以較慢者的速度為準。Bono需花1分鐘過橋,Edge需花2分鐘過橋,Adam需花5分鐘過橋,Larry需花10分鐘過橋。
他們要如何在17分鐘內過 橋呢?
A:
2+1先過 2
然後1回來送手電筒 1
5+10再過 10
2回來送手電筒 2
2+1過去 2
總共2+1+10+2+2=17分鐘
【22】一個家庭有兩個小孩,其中有一個是女孩,問另一個也是女孩的概率(假定生男生女的概率一樣) 1/3A: 樣本空間為(男男)(女女)(男女)(女男)
A=(已知其中一個是女孩)=)(女女)(男女)(女男)
B=(另一個也是女孩)=(女女)
於是P(B/A)=P(AB)/P(A)=(1/4)/(3/4)=1/3
【23】為什麼下水道的蓋子是圓的?
A:不會掉下去
【24】有7克、2克砝碼各一個,天平一隻,如何只用這些物品三次將140克的鹽分成50、90克各一份?
A:
140->70+70 70->35+35
35+70=105
105->50+7 + 55+2
55+35=90
【25】晶片測試:有2k塊晶片,已知好晶片比壞晶片多.請設計
演算法從其中找出一片 好晶片,說明你所用的比較次數上限. 其中:好晶片和其它晶片比較時,能正確給出另一塊晶片是好還是壞. 壞晶片和其它晶片比較時,會隨機的給出好或是壞。A:把第一塊晶片與其它逐一對比,看看其它晶片對第一塊晶片給出的是好是壞,如果給出是好的過半,那麼說明這是好晶片,完畢。如果給出的是壞的過半,說明第一塊晶片是壞的,那麼就要在那些在給出第一塊晶片是壞的晶片中,重複上述步驟,直到找到好的晶片為止。
【26】12個球一個天平,現知道只有一個和其它的重量不同,問怎樣稱才能用三次就找到那個球。13個呢?(注意此題並未說明那個球的重量是輕是重)A:12個時可以找出那個是重還是輕,13個時只能找出是哪個球,輕重不知。
把球編為①②③④⑤⑥⑦⑧⑨⑩⑾⑿。(13個時編號為⒀)
第一次稱:先把①②③④與⑤⑥⑦⑧放天平兩邊,
㈠如相等,說明特別球在剩下4個球中。
把①⑨與⑩⑾作第二次稱量,
⒈如相等,說明⑿特別,把①與⑿作第三次稱量即可判斷是⑿是重還是輕
⒉如①⑨<⑩⑾說明要麼是⑩⑾中有一個重的,要麼⑨是輕的。
把⑩與⑾作第三次稱量,如相等說明⑨輕,不等可找出誰是重球。
⒊如①⑨>⑩⑾說明要麼是⑩⑾中有一個輕的,要麼⑨是重的。
把⑩與⑾作第三次稱量,如相等說明⑨重,不等可找出誰是輕球。
㈡如左邊<右邊,說明左邊有輕的或右邊有重的
把①②⑤與③④⑥做第二次稱量
⒈如相等,說明⑦⑧中有一個重,把①與⑦作第三次稱量即可判斷是⑦與⑧中誰是重球
⒉如①②⑤<③④⑥說明要麼是①②中有一個輕的,要麼⑥是重的。
把①與②作第三次稱量,如相等說明⑥重,不等可找出誰是輕球。
⒊如①②⑤>③④⑥說明要麼是⑤是重的,要麼③④中有一個是輕的。
把③與④作第三次稱量,如相等說明⑤重,不等可找出誰是輕球。
㈢如左邊>右邊,參照㈡相反進行。
當13個球時,第㈠步以後如下進行。
把①⑨與⑩⑾作第二次稱量,
⒈如相等,說明⑿⒀特別,把①與⑿作第三次稱量即可判斷是⑿還是⒀特別,但判斷不了輕重了。
⒉不等的情況參見第㈠步的⒉⒊
【27】100個人回答五道試題,有81人答對第一題,91人答對第二題,85人答對第三題,79人答對第四題,74人答對第五題,答對三道題或三道題以上的人算及格, 那麼,在這100人中,至少有( )人及格。
A:
2+1先過 2
然後1回來送手電筒 1
5+10再過 10
2回來送手電筒 2
2+1過去 2
總共2+1+10+2+2=17分鐘
【22】一個家庭有兩個小孩,其中有一個是女孩,問另一個也是女孩的概率(假定生男生女的概率一樣) 1/3A: 樣本空間為(男男)(女女)(男女)(女男)
A=(已知其中一個是女孩)=)(女女)(男女)(女男)
B=(另一個也是女孩)=(女女)
於是P(B/A)=P(AB)/P(A)=(1/4)/(3/4)=1/3
【23】為什麼下水道的蓋子是圓的?
A:不會掉下去
【24】有7克、2克砝碼各一個,天平一隻,如何只用這些物品三次將140克的鹽分成50、90克各一份?
A:
140->70+70 70->35+35
35+70=105
105->50+7 + 55+2
55+35=90
【25】晶片測試:有2k塊晶片,已知好晶片比壞晶片多.請設計
演算法從其中找出一片 好晶片,說明你所用的比較次數上限. 其中:好晶片和其它晶片比較時,能正確給出另一塊晶片是好還是壞. 壞晶片和其它晶片比較時,會隨機的給出好或是壞。A:把第一塊晶片與其它逐一對比,看看其它晶片對第一塊晶片給出的是好是壞,如果給出是好的過半,那麼說明這是好晶片,完畢。如果給出的是壞的過半,說明第一塊晶片是壞的,那麼就要在那些在給出第一塊晶片是壞的晶片中,重複上述步驟,直到找到好的晶片為止。
【26】12個球一個天平,現知道只有一個和其它的重量不同,問怎樣稱才能用三次就找到那個球。13個呢?(注意此題並未說明那個球的重量是輕是重)A:12個時可以找出那個是重還是輕,13個時只能找出是哪個球,輕重不知。
把球編為①②③④⑤⑥⑦⑧⑨⑩⑾⑿。(13個時編號為⒀)
第一次稱:先把①②③④與⑤⑥⑦⑧放天平兩邊,
㈠如相等,說明特別球在剩下4個球中。
把①⑨與⑩⑾作第二次稱量,
⒈如相等,說明⑿特別,把①與⑿作第三次稱量即可判斷是⑿是重還是輕
⒉如①⑨<⑩⑾說明要麼是⑩⑾中有一個重的,要麼⑨是輕的。
把⑩與⑾作第三次稱量,如相等說明⑨輕,不等可找出誰是重球。
⒊如①⑨>⑩⑾說明要麼是⑩⑾中有一個輕的,要麼⑨是重的。
把⑩與⑾作第三次稱量,如相等說明⑨重,不等可找出誰是輕球。
㈡如左邊<右邊,說明左邊有輕的或右邊有重的
把①②⑤與③④⑥做第二次稱量
⒈如相等,說明⑦⑧中有一個重,把①與⑦作第三次稱量即可判斷是⑦與⑧中誰是重球
⒉如①②⑤<③④⑥說明要麼是①②中有一個輕的,要麼⑥是重的。
把①與②作第三次稱量,如相等說明⑥重,不等可找出誰是輕球。
⒊如①②⑤>③④⑥說明要麼是⑤是重的,要麼③④中有一個是輕的。
把③與④作第三次稱量,如相等說明⑤重,不等可找出誰是輕球。
㈢如左邊>右邊,參照㈡相反進行。
當13個球時,第㈠步以後如下進行。
把①⑨與⑩⑾作第二次稱量,
⒈如相等,說明⑿⒀特別,把①與⑿作第三次稱量即可判斷是⑿還是⒀特別,但判斷不了輕重了。
⒉不等的情況參見第㈠步的⒉⒊
【27】100個人回答五道試題,有81人答對第一題,91人答對第二題,85人答對第三題,79人答對第四題,74人答對第五題,答對三道題或三道題以上的人算及格, 那麼,在這100人中,至少有( )人及格。
A:
首先求解原題。每道題的答錯人數為(次序不重要):26,21,19,15,9
第3分佈層:答錯3道題的最多人數為:(26+21+19+15+9)/3=30
第2分佈層:答錯2道題的最多人數為:(21+19+15+9)/2=32
第1分佈層:答錯1道題的最多人數為:(19+15+9)/1=43
Max_3=Min(30, 32, 43)=30。因此答案為:100-30=70。
其實,因為26小於30,所以在求出第一分佈層後,就可以判斷答案為70了。
要讓及格的人數最少,就要做到兩點:
1. 不及格的人答對的題目儘量多,這樣就減少了及格的人需要答對的題目的數量,也就只需要更少的及格的人
2. 每個及格的人答對的題目數儘量多,這樣也能減少及格的人數
由1得每個人都至少做對兩道題目
由2得要把剩餘的210道題目分給其中的70人: 210/3 = 70,讓這70人全部題目都做對,而其它30人只做對了兩道題
也很容易給出一個具體的實現方案:
讓70人答對全部五道題,11人僅答對第一、二道題,10人僅答對第二、三道題,5人答對第三、四道題,4人僅答對第四、五道題
顯然稍有變動都會使及格的人數上升。所以最少及格人數就是70人!
【28】陳奕迅有首歌叫十年呂珊有首歌叫3650夜那現在問,十年可能有多少天?A:
十年可能包含2-3個閏年,3652或3653天。
1900年這個閏年就是28天,1898~1907這10年就是3651天,閏年如果是整百的倍數,如1800,1900,那麼這個數必須是400的倍數才有29天,比如1900年2月有28天,2000年2月有29天。
【29】 1,11,21,1211,111221,下一個數是什麼?
+1 頭+1 2個1 +2個1 頭+1 ???
A:
下行是對上一行的解釋 所以新的應該是3個1 2個2 1個1 :312211
【30】燒一根不均勻的繩要用一個小時,如何用它來判斷半個小時?
燒一根不均勻的繩,從頭燒到尾總共需要1個小時。現在有若干條材質相同的繩子,問如何用燒繩的方法來計時一個小時十五分鐘呢? (微軟的筆試題)
A:
一,一根繩子從兩頭燒,燒完就是半個小時。
二,一根要一頭燒,一根從兩頭燒,兩頭燒完的時候(30分),將剩下的一根另一端點著,燒盡就是45分鐘。再從兩頭點燃第三根,燒盡就是1時15分。
A:
一,一根繩子從兩頭燒,燒完就是半個小時。
二,一根要一頭燒,一根從兩頭燒,兩頭燒完的時候(30分),將剩下的一根另一端點著,燒盡就是45分鐘。再從兩頭點燃第三根,燒盡就是1時15分。
燒1H(一條繩子燒一頭)同時燒30分(一條繩子燒一半)+15分(在將以燒的一半燒完)
【31】共有三類藥,分別重
1g,2g,3g,放到若干個瓶子中,現在能確定每個瓶子中只有其中一種藥,且每瓶中的藥片足夠多,能只稱一次就知道各個瓶子中都是盛的哪類藥嗎?如果有4類藥呢?5類呢?N類呢(N可數)?如果是共有m個瓶子盛著n類藥呢(m,n為正整數,藥的質量各不相同但各種藥的質量已知)?你能只稱一次就知道每瓶的藥是什麼嗎?A:
注:當然是有代價的,稱過的藥我們就不用了
第一個瓶子拿出一片,第二個瓶子拿出四片,第三個拿出十六片,……第m個拿出n+1的m-1次方片。把所有這些藥片放在一起稱重量。
【32】假設在桌上有三個密封的盒,一個盒中有2枚銀幣(1銀幣=10便士),一個盒中有2枚鎳幣(1鎳幣=5便士),還有一個盒中有1枚銀幣和1枚鎳幣。這些盒子被標上10便士、 15便士和20便士,但每個標籤都是錯誤的。允許你從一個盒中拿出1枚硬幣放在盒前,看到這枚硬幣,你能否說出每個盒內裝的東西呢?A:
取出標著15便士的盒中的一個硬幣,如果是銀的說明這個盒是20便士的,如果是鎳的說明這個盒是10便士的,再由每個盒的標籤都是錯誤的可以推出其它兩個盒裡的東西。
【33】有一個大西瓜,用水果刀平整地切,總共切9刀,最多能切成多少份,最少能切成多少份?主要是過程,結果並不是最重要的
A:
最少10,最多130
見下表,表中藍色部分服從2為底的指數函式規律,紅色部分的數值均為其左邊與左上角的兩個數之和。
x 0 1 2 3 4 5 6 7 8 9
x個點最多能把直線分成多少部分 1 2 3 4 5 6 7 8 9 10
x條直線最多能把平面分成多少部分 1 2 4 7 11 16 22 29 37 46
x個平面最多能把空間分成多少部分 1 2 4 8 15 26 42 64 93 130
【34】一個巨大的圓形水池,周圍佈滿了老鼠洞。貓追老鼠到水池邊,老鼠未來得及進洞就掉入水池裡。貓繼續沿水池邊緣企圖捉住老鼠(貓不入水)。已知V貓=4V鼠。問老鼠是否有辦法擺脫貓的追逐?A:
第一步:游到水池中心。
第二步:從水池中心遊到距中心R/4處,並始終保持鼠、水池中心、貓在一直線上。
第三步:沿與中心相反方向的直線遊3R/4就可以到達水池邊,而貓沿圓周到達那裡需要3.14R,所以捉不到老鼠。
三個階段如下圖所示:
【35】有三個桶,兩個大的可裝8斤的水,一個小的可裝3斤的水,現在有16斤水裝滿了兩大桶就是8斤的桶,小桶空著,如何把這16斤水分給4個人,每人4斤。沒有其他任何工具,4人自備容器,分出去的水不可再要回來。
A:
表示為880,接下來,將一個大桶的水倒入小桶中,倒滿,表示為853,(第2個大桶減3,小桶加3)則過程如下:
880——853:將3斤給第1個人,變為850(此時
4人分別有水3-0-0-0)
850——823:將2斤給第2個人,變為803(此時4人分別有水3-2-0-0)
803——830——533——560——263——281:將1斤給第1個人,變為280(此時4人分別有水4-2-0-0)
280——253——703——730——433——460——163:將1斤給第3個人,變為063(此時4人分別有水4-2-1-0)
063——081:將1斤給第4個人,變為080(此時4人分別有水4-2-1-1)
080——053——350——323:將2斤給第2個人,將2個3斤分別給第3、4個人,(此時4人分別有水4-4-4-4)
【36】從前有一位老鐘錶匠,為一個教堂裝一隻大鐘。他年老眼花,把長短針裝配錯了,短針走的速度反而是長針的12倍。裝配的時候是上午6點,他把短針指在“6 ”上,長針指在“12”上。老鐘錶匠裝好就回家去了。人們看這鐘一會兒7點,過了不一會兒就8點了,都很奇怪,立刻去找老鐘錶匠。等老鐘錶匠趕到,已經是下午7點多鐘。他掏出懷錶來一對,鍾準確無誤,疑心人們有意捉弄他,一生氣就回去了。這鐘還是8點、9點地跑,人們再去找鐘錶匠。老鐘錶匠第二天早晨8點多趕來用表一對,仍舊準確無誤。請你想一想,老鐘錶匠第一次對錶的時候是7點幾分?第二次對錶又是8點幾分?
A:
7點x分:(7+x/60)/12=x/60 x=7*60=420/11=38.2
第一次是7點38分,第二次是8點44分
【37】今有2匹馬、3頭牛和4只羊,它們各自的總價都不滿10000文錢(古時的貨幣單位)。如果2匹馬加上1頭牛,或者3 頭牛加上1只羊,或者4只羊加上1匹馬,那麼它們各自的總價都正好是10000文錢了。問:馬、牛、羊的單價各是多少文錢?
A:
【37】今有2匹馬、3頭牛和4只羊,它們各自的總價都不滿10000文錢(古時的貨幣單位)。如果2匹馬加上1頭牛,或者3 頭牛加上1只羊,或者4只羊加上1匹馬,那麼它們各自的總價都正好是10000文錢了。問:馬、牛、羊的單價各是多少文錢?
A:
X馬3600 Y牛 2800 Z羊1600
【38】一天,harlan的店裡來了一位顧客,挑了25元的貨,顧客拿出100元,harlan沒零錢找不開,就到隔壁飛白的店裡把這100元換成零錢,回來給顧客找了75元零錢。過一會,飛白來找harlan,說剛才的是假錢,harlan馬上給飛白換了張真錢,問harlan賠了多少錢?
A:
100元(貨25元+找給顧客75元=100元)
【39】猴子爬繩這道力學怪題乍看非常簡單,可是據說它卻使劉易斯.卡羅爾感到困惑。至於這道怪題是否由這位因《愛麗絲漫遊奇境記》而聞名的牛津大學數學專家提出來的,那就不清楚了。總之,在一個不走運的時刻,他就下述問題徵詢人們的意見:一根繩子穿過無摩擦力的滑輪,在其一端懸掛著一隻10磅重的砝碼,繩子的另一端有隻猴子,同砝碼正好取得平衡。當猴子開始向上爬時,砝碼將如何動作呢?"真奇怪,"卡羅爾寫道,"許多優秀的數學家給出了截然不同的答案。普賴斯認為砝碼將向上升,而且速度越來越快。克利夫頓(還有哈考特)則認為,砝碼將以與猴子一樣的速度向上升起,然而桑普
森卻說,砝碼將會向下降!"一位傑出的機械工程師說"這不會比蒼蠅在繩子上爬更起作用",而一位科學家卻認為"砝碼的上升或下降將取決於猴子吃蘋果速度的倒數",然而還得從中求出猴子尾巴的平方根。嚴肅地說,這道題目非常有趣,值得認真推敲。它很能說明趣題與力學問題之間的緊密聯絡。
A:
砝碼將以與猴子相同的速度上升,因為它們質量相同,受力也相同。
【40】兩個空心球,大小及重量相同,但材料不同。一個是金,一個是鉛。空心球表面圖有相同顏色的油漆。現在
要求在不破壞表面油漆的條件下用簡易方法指出哪個是金的,哪個是鉛的。
A:
旋轉看速度,金的密度大,質量相同,所以金球的實際體積較小,因為外半徑相同,所以金球的內半徑較大,所以金球的轉動慣量大,在相同的外加力矩之下,金球的角加速度較小,所以轉得慢。
【41】有23枚硬幣在桌上,10枚正面朝上。假設別人矇住你的眼睛,而你的手又摸不出硬幣的反正面。讓你用最好的方法把這些硬幣分成兩堆,每堆正面朝上的硬幣個數相同。
A:
分成10+13兩堆, 然後翻轉10的那堆
【42】三個村莊A、B、C和三個城鎮A、B、C坐落在如圖所示的環形山內。由於歷史原因,只有同名的村與鎮之間才有來往。為方便交通,他們準備修鐵路。問題是:如何在這個環形山內修三條鐵路連通A村與A鎮, B村與B鎮,C村與C鎮。而這些鐵路相互不能相交。(挖山洞、修立交橋都不算,絕對是平面問題)。想出答案再想想這個題說明什麼問題。
答案如右圖:
【43】屋裡三盞燈泡,屋外三個開關,一個開關僅控制一盞燈,屋外看不到屋裡怎樣只進屋一次,就知道哪個開關控制哪盞燈?四盞呢~
溫度,先開一盞,足夠長時間後關了,開另一盞,進屋看,亮的為後來開的,摸起來熱的為先開的,剩下的一盞也就確定了。
四盞的情況:設四個開關為ABCD,先開AB,足夠長時間後關B開C,然後進屋,又熱又亮為A,只熱不亮為B,只亮不熱為C,不亮不熱為D。
【44】2+7-2+7全部有火柴根組成,移動其中任何一根,答案要求為30
A:
說明:因為書寫問題作如下解釋,2是由橫折橫三根組成,7是由橫折兩根組成
1, 改變賦值號.比如+,-,=
2, 注意質數.
3, 可能把畫面顛倒過來.
4, 然後就可以去考慮更改其他數字更改了
247-217=30
【45】5名海盜搶得了窖藏的100塊金子,並打算瓜分這些戰利品。這是一些講民主的海盜(當然是他們自己特有的民主),他們的習慣是按下面的方式進行分配:最厲害的一名海盜提出分配方案,然後所有的海盜(包括提出方案者本人)就此方案進行表決。如果50%或更多的海盜贊同此方案,此方案就獲得通過並據此分配戰利品。否則提出方案的海盜將被扔到海里,然後下一名最厲害的海盜又重複上述過程。所有的海盜都樂於看到他們的一位同夥被扔進海里,不過,如果讓他們選擇的話,他們還是寧可得一筆現金。他們當然也不願意自己被扔到海里。所有的海盜都是有理性的,而且知道其他的海盜也是有理性的。此外,沒有兩名海盜是同等厲害的——這些海盜按照完全由上到下的等級排好了座次,並且每個人都清楚自己和其他所有人的等級。這些金塊不能再分
,也不允許幾名海盜共有金塊,因為任何海盜都不相信他的同夥會遵守關於共享金塊的安排。這是一夥每人都只為自己打算的海盜。最凶的一名海盜應當提出什麼樣的分配方案才能使他獲得最多的金子呢?
如果輪到第四個海盜分配:100,0
輪到第三個:99,0,1
輪到第二個:98,0,1,0
輪到第一個:97,0,1,0,2,這就是第一個海盜的最佳方案。
【46】他們中誰的存活機率最大?
5個囚犯,分別按1-5號在裝有100顆綠豆的麻袋抓綠豆,規定每人至少抓一顆,而抓得最多和最少的人將被處死,而且,他們之間不能交流,但在抓的時候,可以摸出剩下的豆子數。問他們中誰的存活機率最大?
A:
提示:
1,他們都是很聰明的人
2,他們的原則是先求保命,再去多殺人
3,100顆不必都分完
4,若有重複的情況,則也算最大或最小,一併處死
第一個人選擇17時最優的。它有先動優勢。他確實有可能被逼死,後面的2、3、4號也想把1號逼死,但做不到(起碼確定性逼死做不到)
可以看一下,如果第1個人選擇21,他的資訊時暴露給第2個人的,那麼,1號就將自己暴露在一個非常不利的環境下,2-4號就會選擇20,五號就會被迫在1-19中選擇,則1、5號處死。所以1號不會這樣做,會選擇一個更小的數。
1號選擇一個
下面決定的就是1號會選擇一個什麼數,他仍然不會選擇一個太大或太小的數,因為那樣仍然是自己處於不利的地位(2-4號肯定不會留情面的),100/6=16.7(為什麼除以6?因為5號會隨機選擇一個數,對1號來說要儘可能的靠近中央,2-4好也是如此,而且正因為2-4號如此,1號才如此... ...),最終必然是在16、17種選擇的問題。
對16、17進行概率的計算之後,就得出了3個人選擇17,第四個人選擇16時,為均衡的狀態,第4號雖然選擇16不及前三個人選擇17生存的機會大,但是若選擇17則整個遊戲的人必死(包括他自己
)!第3號沒有動力選擇16,因為計算概率可知生存機會不如17。
所以選擇為17、17、17、16、X(1-33隨機),1-3號生存機會最大。
【47】有5只猴子在海邊發現 一堆桃子,決定第二天來平分.第二天清晨,第一隻猴子最早來到,它左分右分分不開,就朝海里扔了一隻,恰好可以分成5份,它拿上自己的一份走了.第 2,3,4,5只猴子也遇到同樣的問題,採用了同樣的方法,都是扔掉一隻後,恰好可以分成5份.問這堆桃子至少有多少隻?
A: 這堆桃子至少有3121只。
第一隻猴子扔掉1個,拿走624個,餘2496個;
第二隻猴子扔掉1個,拿走499個,餘1996個;
第三隻猴子扔掉1個,拿走399個,餘1596個;
第四隻猴
子扔掉1個,拿走319個,餘1276個;
第五隻猴子扔掉1個,拿走255個,餘4堆,每堆255個。
如果不考慮正負,-4為一解
考慮到要5個猴子分,假設分n次。
則題目的解: 5^n-4
本題為5^5-4=3121.
設共a個桃,剩下b個桃,則b=(4/5)((4/5)((4/5)((4/5)((4/5)(a-1)-1)-1)-1)-1)-1),即b=(1024a-8404)/3125 ; a=3b+8+53*(b+4)/1024,而53跟1024不可約,則令b=1020可有最小解,得a=3121 ,設桃數x,得方程
4/5{4/5{4/5[4/5(x-1)-1]-1}-1}=5n
展開得
256x=3125n+2101
故x=(3125n+2101)/256=12n+8+53*(n+1)/256
因為53與256不可約,所以判斷n=255有一解.x為整數,等於3121
【48】話說某天一艘海盜船被天下砸下來的一頭牛給擊中了,5個倒黴的傢伙只好逃難到一個孤島,發現島上孤零零的,幸好有有棵椰子樹,還有一隻猴子!大家把椰子全部採摘下來放在一起,但是天已經很晚了,所以就睡覺先.
晚上某個傢伙悄悄的起床,悄悄的將椰子分成5份,結果發現多一個椰子,順手就給了幸運的猴子,然後又悄悄的藏了一份,然後把剩下的椰子混在一起放回原處,最後還是悄悄滴回去睡覺了.
過了會兒,另一個傢伙也悄悄的起床,悄悄的將剩下的椰子分成5份,結果發現多一個椰子,順手就又給了幸運的猴子,然後又悄悄滴藏了一份,把剩下的椰子混在一起放回原處,最後還是悄悄滴回去睡覺了.
又過了一會 ......
又過了一會 ...
總之5個傢伙都起床過,都做了一樣的事情。早上大家都起床,各自心懷鬼胎的分椰子了,這個猴子還真不是一般的幸運,因為這次把椰子分成5分後居然還是多一個椰子,只好又給它了.問題來了,這堆椰子最少有多少個?
A: 這堆椰子最少有15621
第一個人給了猴子1個,藏了3124個,還剩12496個;
第二個人給了猴子1個,藏了2499個,還剩9996個;
第三個人給了猴子1個,藏了1999個,還剩7996個;
第四個人給了猴子1個,藏了1599個,還剩6396個;
第五個人給了猴子1個,藏了1279個,還剩5116個;
最後大家一起分成5份,每份
1023個,多1個,給了猴子。
【49】小明和小強都是張老師的學生,張老師的生日是M月N日,2人都知道張老師的生日是下列10組中的一天,張老師把M值告訴了小明,把N值告訴了小強,張老師問他們知道他的生日是那一天嗎?
3月4日 /3月5日/ 3月8日 / 6月4日 /6月7日/9月1日 /9月5日
12月1日/ 12月2日/ 12月8日
M小明說:如果我不知道的話,小強肯定也不知道
N小強說:本來我也不知道,但是現在我知道了
小明說:哦,那我也知道了
請根據以上對話推斷出張老師的生日是哪一天
A: 9.1
【50】一邏輯學家誤入某部落,被囚於牢獄,酋長欲意放行,他對邏輯學家說:“今有兩門,一為自由,一為死亡,你可任意開啟一門。
現從兩個戰士中選擇一人負責解答你所提的任何一個問 題(Y/N),其中A一個天性誠實,B一人說謊成性,今後生死任你選擇。”邏輯學家沉思片刻,即向一戰士發問,然後開門從容離去。
A: (問A自由門在那裡或問B死亡之門在那裡)
邏輯學家應如何發問?
問:如果我問另一個人死亡之門在哪裡,他會怎麼回答?
最終得到的回答肯定是指向自由之門的。
【51】說從前啊,有一個富 人,他有30個孩子,其中15個是已故的前妻所生,其餘15個是繼室所生,這後一個婦人很想讓她自己所生的最年長的兒子繼承財產,於是,有一天,他就向他 說:"親愛的丈夫啊,你就要老了,我們應該定下來誰將是你的繼承人,讓我們把我們的30個孩子排成一個圓圈,從他們中的一個數起,每逢到10就讓那個孩子 站出去,直到最後剩下哪個孩子,哪個孩子就繼承你的財產吧!"富人一想,我靠,這個題意相當有內涵了,不錯,彷彿很公平,就這麼辦吧~不過,當剔選過程不 斷進行下去的時候,這個富人傻眼了,他發現前14個被剔除的孩子都是前妻生的,而且下一個要被剔除的還是前妻生的,富人馬上大手一揮,停,現在從這個孩子 倒回去數, 繼室,就是這個歹毒的後媽一想,倒數就倒數,我15個兒子還鬥不過你一個啊~她立即同意了富人的動議,你猜,到底誰做了繼承人呢~
A: 老婆的兒子
【52】“有一牧場,已知養牛27頭,6天把草吃盡;養牛23頭,9天把草吃盡。如果養牛21頭,那麼幾天能把牧場上的草吃盡呢?並且牧場上的草是不斷生長的。”
A:
設牛每天吃掉x,草每天長出y,原來有牧場的草量是a
a=(27x-y)*6=(23x-y)*9
可解出y=15x, a=72x,所以a=(21x-y)*Z
72x=(21x-y)*Z ==> 72x=(21x-15x)*Z==>72X=6X*Z
Z=12 ,所以需要12天。
【53】一個商人騎一頭驢要穿越1000公里長的沙漠,去賣3000根胡蘿蔔。已知驢一次性可馱1000根胡蘿蔔,但每走一公里又要吃掉一根胡蘿蔔。問:商人共可賣出多少胡蘿蔔?
A:
商人帶驢馱1000根胡蘿蔔,先走250公里,這時,驢已吃250根,放下500根,原地返回,又吃掉250根。商人再帶驢馱1000根胡蘿蔔,走到250公里處,這時,驢已吃250根,再馱上原先放的500根中的250根,繼續前行至500公里處,這時,驢又吃250根,放下500根,剩250根返回250公里處,在馱上250公里處剩下的250根返回原地,這時驢又吃250根。
商人再帶驢馱1000根胡蘿蔔,走到500公里處,這時,驢已吃500根,再馱上原先放的500根,走出沙漠,驢吃掉500根,還剩500根。
【54】10箱黃金,每箱100塊,每塊一兩。有貪官,把某一箱的每塊都磨去一錢。請稱一次找到不足量的那個箱子
A:
第一箱子拿1塊,第二箱子拿2塊, 第10箱子拿10塊,然後放在一起稱,看看缺了幾錢,缺了n錢就說明是第n個箱子
【55】你讓工人為你工作7天,給工人的回報是一根金條。金條平分成相連的7段,你必須在每天結束時都付費,如果只許你兩次把金條弄斷,你如何給你的工人付費?
A:
把金條分成1,2,4三段。第一天1,第二天2,第三天1+2……第七天1+2+4。
【56】有十瓶藥,每瓶裡都裝有100片藥(彷彿現在裝一百片的少了,都是十片二十片的,不管,咱們就這麼來了),其中有八瓶裡的藥每片重10克,另有兩瓶裡的藥每片重9克。用一個蠻精確的小秤,只稱一次,如何找出份量較輕的那兩個藥瓶?
等同54,但此題有一些變化,與眾不同的瓶子有兩個,只稱一次的話,只能得到兩個瓶子所缺的克數的總和,我們必須保證能從總和中唯一地得出兩個瓶子的所缺數。第一個瓶可拿出1片,第二個拿2片,第三個拿3片,但第四個不能拿4片,因為如果結果缺了5克的話,你就不知道是缺了2+3還是1+4。所以第四個應拿5片,第五個應拿8片,第n個應拿a(n-1)+a(n-2)片。
【57】一個經理有三個女兒, 三個女兒的年齡加起來等於13,三個女兒的年齡乘起來等於經理自己的年齡,有一個下屬已知道經理的年齡,但仍不能確定經理三個女兒的年齡,這時經理說只有,一個女兒的頭髮是黑的,然後這個下屬就知道了經理三個女兒的年齡。請問三個女兒的年齡分別是多少?為什麼?
A:
顯然3個女兒的年齡都不為0,要不爸爸就為0歲了,因此女兒的年齡都大於等於1歲。這樣可以得下面的情況:1*1*11=11,1*2**10=20,1*3*9=27,1*4*8=32,1*5*7=35,{1*6*6=36},{2*2*9=36},2*3*8=48,2*4*7=56,2*5*6=60,3*3*7=63,3*4*6=72,3*5*5=75,4*4*5=80因為下屬已知道經理的年齡,但仍不能確定經理三個女兒的年齡,說明經理是36歲(因為{1*6*6=36},{2*2*9=36}),所以3個女兒的年齡只有2種情況,經理又說只有一個女兒的頭髮是黑的,說明只有一個女兒是比較大的,其他的都比較小,頭髮還沒有長成
黑色的,所以3個女兒的年齡分別為2,2,9!
【58】有三個人去住旅館,住 三間房,每一間房?元,於是他們一共付給老闆?,第二天,老闆覺得三間房只需要?元就夠了於是叫小弟退回?給三位客人,誰知小弟貪心,只退 回每人?,自己偷偷拿了ū,這樣一來便等於那三位客人每人各花了九元,於是三個人一共花了?,再加上小弟獨吞了不ū,總共是?。可是當初他 們三個人一共付出?那麼還有?呢?
應該是三個人付了9*3=27,其中2付給了小弟,25付給了老闆
【59】有兩位盲人,他們都各自買了兩對黑襪和兩對白襪,八對襪了的布質、大小完全相同,而每對襪了都有一張商標紙連著。兩位盲人不小心將八對襪了混在一起。他們每人怎樣才能取回黑襪和白襪各兩對呢?
A:
拆開所有的襪子,每人一個
【60】有一輛火車
以每小時 15公里的速度離開洛杉磯直奔紐約,另一輛火車以每小時20公里的速度從紐約開往洛杉磯。如果有一隻鳥,以30公里每小時的速度和兩輛火車同時啟動,從洛杉磯出發,碰到另一輛車後返回,依次在兩輛火車來回飛行,直到兩輛火車相遇,請問,這隻小鳥飛行了多長距離?
設總距離為d,總共用時d/(15+20),兩車相遇,所以鳥飛了30*d/(15+20)=6d/7
【61】你有兩個罐子,每個罐子各有若干紅色彈球和藍色彈球,兩個罐子共有50個紅色彈球,50個藍色彈球,隨機選出一個罐子,隨機從中選取出一個彈球,要使取出的是紅球的概率最大,一開始兩個罐子應放幾個紅球,幾個藍球?在你的計劃中,得到紅球的準確機率是多少?
一個罐子放1紅,一個罐子放49紅和50藍,這樣得到紅球的概率接近3/4。
【62】你有四個裝藥丸的罐子,每個藥丸都有一定的重量,被汙染的藥丸是沒被汙染的重量+1.只稱量一次,如何判斷哪個罐子的藥被汙染了?
與前面的54,56題相似。
【63】對一批編號為1~100,全部開關朝上(開)的燈進行以下操作:凡是1的倍數反方向撥一次開關;2的倍數反方向又撥一次開關;3的倍數反方向又撥一次開關……問:最後為關熄狀態的燈的編號。
A:
1 4 9
【64】想象你在鏡子前,請問,為什麼鏡子中的影像可以顛倒左右,卻不能顛倒上下?
A:
實際上鏡子並沒有顛倒左右,而是顛倒前後。
【65】一群人開舞會,每人頭 上都戴著一頂帽子。帽子只有黑白兩種,黑的至少有一頂。每個人都能看到其它人帽子的顏色,卻看不到自己的。主持人先讓大家看看別人頭上戴的是什么帽子,然 後關燈,如果有人認為自己戴的是黑帽子,就打自己一個耳光。第一次關燈,沒有聲音。於是再開燈,大家再看一遍,關燈時仍然鴉雀無聲。一直到第三次關燈,才 有劈劈啪啪打耳光的聲音響起。問有多少人戴著黑帽子?
3 。如果只有1人戴黑帽子,那麼第一次關燈他就會打自己耳光;如果有2人,第二次關燈他們就會打自己耳光;有n人戴帽子的話第n次關燈他們就會打自己耳光。
【66】兩個圓環,半徑分別是1和2,小圓在大圓內部繞大圓圓周一週,問小圓自身轉了幾周?如果在大圓的外部,小圓自身轉幾周呢?
把大圓剪斷拉直。小圓繞大圓圓周一週,就變成從直線的一頭滾至另一頭。因為直線長就是大圓的周長,是小圓周長的2倍,所以小圓要滾動2圈。
但是現在小圓不是沿直線而是沿大圓滾動,小圓因此還同時作自轉,當小圓沿大圓滾動1週迴到原出發點時,小圓同時自轉1周。當小圓在大圓內部滾動時自轉的方向與滾動的轉向相反,所以小圓自身轉了
1周。當小圓在大圓外部滾動時自轉的方向與滾動的轉向相同,所以小圓自身轉了3周。
這一題非常有迷惑性,小圓在外部時其實是3圈,你可以拿個硬幣試試可以把圓看成一根繩子,長繩是短繩的2倍長,假設長繩開始介面在最底下,短繩介面在長繩介面處,然後短繩開始順時針繞,當短繩介面對著正左時,這時其實才繞了長繩的1/4,轉了180+90度,所以繞一圈是270*4=360*3 。同理小圓在內部時是1圈。也可以套用下列公式: 兩圓圓心距/轉動者半徑=轉動者切另一圓時的自轉數!!
【67】 1元錢一瓶汽水,喝完後兩個空瓶換一瓶汽水,問:你有20元錢,最多可以喝到幾瓶汽水?
A:
40瓶,
20+10+5+2+1+1=39, 這時還有一個空瓶子,先向店主借一個空瓶,換來一瓶汽水喝完後把空瓶還給店主。
【68】有3頂紅帽子,4頂黑 帽子,5頂白帽子。讓10個人從矮到高站成一隊,給他們每個人頭上戴一頂帽子。每個人都看不見自己戴的帽子的顏色,卻只能看見站在前面那些人的帽子顏色。 (所以最後一個人可以看見前面9個人頭上帽子的顏色,而最前面那個人誰的帽子都看不見。現在從最後那個人開始,問他是不是知道自己戴的帽子顏色,如果他回 答說不知道,就繼續問他前面那個人。假設最前面那個人一定會知道自己戴的是黑帽子。為什麼?
“有3頂黑帽子,2頂白帽子。讓三個人從前到後站成一排,給他們每個人頭上戴一頂帽子。每個人都看不見自己戴的帽子的顏色,卻只能看見站在前面那些人的帽子顏色。(所以最後一個人可以看見前面兩個人頭上帽子的顏色,中間那個人看得見前面那個人的帽子顏色但看不見在他後面那個人的帽子顏色,而最前面那個人誰的帽子都看不見。現
在從最後那個人開始,問他是不是知道自己戴的帽子顏色,如果他回答說不知道,就繼續問他前面那個人。事實上他們三個戴的都是黑帽子,那麼最前面那個人一定會知道自己戴的是黑帽子。為什麼?”
答案是,最前面的那個人聽見後面兩個人都說了“不知道”,他假設自己戴的是白帽子,於是中間那個人就看見他戴的白帽子。那麼中間那個人會作如下推理:“假設我戴了白帽子,那麼最後那個人就會看見前面兩頂白帽子,但總共只有兩頂白帽子,他就應該明白他自己戴的是黑帽子,現在他說不知道,就說明我戴了白帽子這個假定是錯的,所以我戴了黑帽子。”問題是中間那人也說不知道,所以最前面那個人知道自己戴白帽子的假定是錯的,所以他推斷出自己戴了黑帽子。
我們把這個問題推廣成如下的形式:
“有若干種顏色的帽子,每種若干頂。假設有若干個人從
前到後站成一排,給他們每個人頭上戴一頂帽子。每個人都看不見自己戴的帽子的顏色,而且每個人都看得見在他前面所有人頭上帽子的顏色,卻看不見在他後面任何人頭上帽子的顏色。現在從最後那個人開始,
問他是不是知道自己戴的帽子顏色,如果他回答說不知道,就繼續問他前面那個人。一直往前問,那麼一定有一個人知道自己所戴的帽子顏色。”
當然要假設一些條件:
1)首先,帽子的總數一定要大於人數,否則帽子都不夠戴。
2)“有若干種顏色的帽子,每種若干頂,有若干人”這個資訊是佇列中所有人都事先知道的,而且所有人都知道所有人都知道此事,所有人都知道所有人都知道所有人都知道此事,等等等等。但在這個條件中的“若干”不一定非要具體一一給出數字來。
這個資訊具體地可以是象上面經典的形式,列舉出每種顏色帽子的數目“有3頂黑帽子,2頂白帽子,3個人”,也可以是“有紅黃綠三種顏色的帽子各1頂2頂3頂,但具體不知道哪種顏色是幾頂,有6個人”,甚至連具體人數也可以不知道,“有不知多少人排成一排,有黑白兩種帽子,每種帽子的數目都比人數少1”,這時候那個排在最後的人並不知道自己排在最後——直到開始問他時發現在他回答前沒有別人被問到,他才知道他在最後。在這個帖子接下去的部分當我出題的時候我將只寫出“有若干種顏色的帽子,每種若干頂,有若干人”這個預設條件,因為這部分確定了,題目也就確定了。
3)剩下的沒有戴在大家頭上的帽子當然都被藏起來了,隊伍裡的人誰都不知道都剩下些什麼帽子。
4)所有人都不是色盲,不但不是,而
且只要兩種顏色不同,他們就能分別出來。當然他們的視力也很好,能看到前方任意遠的地方。他們極其聰明,邏輯推理是極好的。總而言之,只要理論上根據邏輯推導得出來,他們就一定推導得出來。相反地如果他們推不出自己頭上帽子的顏色,任何人都不會試圖去猜或者作弊偷看——不知為不知。
5)後面的人不能和前面的人說悄悄話或者打暗號。
當然,不是所有的預設條件都能給出一個合理的題目。比如有99頂黑帽子,99頂白帽子,2個人,無論怎麼戴,都不可能有人知道自己頭上帽子的顏色。另外,只要不是隻有一種顏色的帽子,在只由一個人組成的隊伍裡,這個人也是不可能說出自己帽子的顏色的。
但是下面這幾題是合理的題目:
1)3頂紅帽子,4頂黑帽子,5頂白帽子,10個人。
2)3頂紅帽子,4頂黑帽子,5頂白帽子,8個人。
3)n頂黑帽子,n-1頂白帽子,n個人(n>0)。
4)1頂顏色1的帽子,2頂顏色2的帽子,…
…,99頂顏色99的帽子,100頂顏色100的帽子,共5000個人。
5)有紅黃綠三種顏色的帽子各1頂2頂3頂,但具體不知道哪種顏色是幾頂,有6個人。
6)有不知多少人(至少兩人)排成一排,有黑白兩種帽子,每種帽子的數目都比人數少1。
大家可以先不看我下面的分析,試著做做這幾題。
如果按照上面3頂黑帽2頂白帽時的推理方法去做,那麼10個人就可以把我們累死,別說5000個人了。但是3)中的n是個抽象的數,考慮一下怎麼解決這個問題,對解決一般的問題大有好處。
假設現在n個人都已經戴好了帽子,問排在最後的那一個人他頭上的帽子是什麼顏色,什麼時候他會回答“知道”?很顯然,只有在他看見前面n-1個人都戴著白帽時才可能,因為這時所有的n-1頂白帽都已用光,在他自己的腦袋上只能頂著黑帽子,只要前面有一頂黑帽子,那麼他就無法排除自己頭上是黑帽子的可能——即使他看見前面所有人都是黑帽,他還是有可能戴著第n頂黑帽。
現在假設最後那個人的回答是“不知道”,那麼輪到問倒數第二人。根據最後面那位的回答,他能推斷出什麼呢?如果他看見的都是白帽,那麼他立刻可以推斷出自己戴的是黑帽——要是他也戴著白帽,那麼最後那人應該看見一片白帽,問到他時他就該回答“知道”了。但是如果倒數第二人看見前面至少有一頂黑帽,他就無法作出判斷——他有可能戴著白帽,但是他前面的那些黑帽使得最後那人無法回答“知道”;他自然也有可能戴著黑帽。
這樣的推理可以繼續下去,但是我們已經看出了苗頭。最後那個人可
以回答“知道”當且僅當他看見的全是白帽,所以他回答“不知道”當且僅當他至少看見了一頂黑帽。這就是所有帽子顏色問題的關鍵!
如果最後一個人回答“不知道”,那麼他至少看見了一頂黑帽,所以如果倒數第二人看見的都是白帽,那麼最後那個人看見的至少一頂黑帽在哪裡呢?不會在別處,只能在倒數第二人自己的頭上。這樣的推理繼續下去,對於佇列中的每一個人來說就成了:
“在我後面的所有人都看見了至少一頂黑帽,否則的話他們就會按照相同的判斷斷定自己戴的是黑帽,所以如果我看見前面的人戴的全是白帽的話,我頭上一定戴著我身後那個人看見的那頂黑帽。”
我們知道最前面的那個人什麼帽子都看不見,就不用說看見黑帽了,所以如果他身後的所有人都回答說“不知道”,那麼按照上面的推理,他可以確定自己戴的是黑帽,因為他身後的人必定看見了一頂黑帽——只能是第一個人他自己頭上的那頂。事實上很明顯,第一個說
出自己頭上是什麼顏色帽子的那個人,就是從隊首數起的第一個戴黑帽子的人,也就是那個從隊尾數起第一個看見前面所有人都戴白帽子的人。
這樣的推理也許讓人覺得有點迴圈論證的味道,因為上面那段推理中包含了“如果別人也使用相同的推理”這樣的意思,在邏輯上這樣的自指式命題有點危險。但是其實這裡沒有迴圈論證,這是類似數學歸納法的推理,每個人的推理都建立在他後面那些人的推理上,而對於最後一個人來說,他的身後沒有人,所以他的推理不依賴於其他人的推理就可以成立,是歸納中的第一個推理。稍微思考一下,我們就可以把上面的論證改得適合於任何多種顏色的推論:
“如果我們可以從假設斷定某種顏色的帽子一定會在佇列中出現,從隊尾數起第一個看不見這種顏色的帽子的人就立刻可以根據和此論證相同的論證來作出判斷,他戴的是這種顏色的帽子。現在所有我身後的人都回答不知道,所以我身後的人也看見了此種顏色的帽子。如果在我前面我見不到此顏色的帽子,那麼一定是我戴著這種顏色的帽子。”
當然第一個人的初始推理相當簡單:“佇列中一定有人戴這種顏色的帽子,現在我看不見前面有人戴這顏色的帽子,那它只能是戴在我的頭上了。”
對於題1)事情就變得很明顯,3頂紅帽子,4頂黑帽子,5頂白帽子給10個人戴,佇列中每種顏色至少都該有一頂,於是從隊尾數起第一個看不見某種顏色的帽子的人就能夠斷定他自己戴著這種顏色的帽子,通過這點我們也可以看到,最多問
到從隊首數起的第三人時,就應該有人回答“知道”了,因為從隊首數起的第三人最多隻能看見兩頂帽子,所以最多看見兩種顏色,如果他後面的人都回答“不知道”,那麼他前面一定有兩種顏色的帽子,而他頭上戴的一定是他看不見的那種顏色的帽子。
題2)也一樣,3頂紅帽子,4頂黑帽子,5頂白帽子給8個人戴,那麼佇列中一定至少有一頂白帽子,因為其它顏色加起來一共才7頂,所以佇列中一定會有人回答“知道”。
題4)的規模大了一點,但是道理和2)完全一樣。100種顏色的5050頂帽子給5000人戴,前面99種顏色的帽子數量是1+……+99=4950,所以佇列中一定有第100種顏色的帽子(至少有50頂),所以如果自己身後的人都回答“不知道”,那麼那個看不見顏色100帽子的人就可以斷定自己戴著這種顏色的帽子。
至於5)、6)“有紅黃綠三種顏色的帽子各1頂2頂3頂,但具體不知道哪種顏色是幾頂,有6個人”以及“有不知多少人排成一排,有黑白兩種帽子,每種帽子的數目都比人數少1”,原理完全相同,
我就不具體分析了。
最後要指出的一點是,上面我們只是論證了,如果我們可以根據各種顏色帽子的數量和佇列中的人數判斷出在佇列中至少有一頂某種顏色的帽子,那麼一定有一人可以判斷出自己頭上的帽子的顏色。因為如果所有身後的人都回答“不知道”的話,那個從隊尾數起第一個看不見這種顏色的帽子的人就可以判斷自己戴了此顏色的帽子。但是這並不是說在詢問中一定是由他來回答“知道”的,因為還可能有其他的方法來判斷自己頭上帽子的顏色。比如說在題2)中,如果佇列如下:(箭頭表示佇列中人臉朝的方向)
白白黑黑黑黑紅紅紅白→
那麼在隊尾第一人就立刻可以回答他頭上的是白帽,因為他看見了所有的3頂紅帽子和4頂黑帽子,能留給他自己戴的只能是白帽子了
【69】假設排列著100個乒乓球,由兩個人輪流拿球裝入口袋,能拿到第100個乒乓球的人為勝利者。條件是:每次拿球者至少要拿1個,但最多不能超過5個,問:如果你是最先拿球的人,你該拿幾個?以後怎麼拿就能保證你能得到第100個乒乓球?
首先拿4個 別人拿n個你就拿6-n個
【70】盧姆教授說:“有一次 我目擊了兩隻山羊的一場殊死決鬥,結果引出了一個有趣的數學問題。我的一位鄰居有一隻山羊,重54磅,它已有好幾個季度在附近山區稱王稱霸。後來某個好事 之徒引進了一隻新的山羊,比它還要重出3磅。開始時,它們相安無事,彼此和諧相處。可是有一天,較輕的那隻山羊站在陡峭的山
路頂上,向它的競爭對手猛撲過 去,那對手站在土丘上迎接挑戰,而挑戰者顯然擁有居高臨下的優勢。不幸的是,由於猛烈碰撞,兩隻山羊都一命嗚呼了。
現在要講一講本題的奇妙之處。對飼養山羊頗有研究,還寫過書的喬治.阿伯克龍比說道:“通過反覆實驗,我發現,動量相當於一個自20英尺高處墜落下來 的30磅重物的一次撞擊,正好可以打碎山羊的腦殼,致它死命。”如果他說得不錯,那麼這兩隻山羊至少要有多大的逼近速度,才能相互撞破腦殼?你能算出來 嗎?
1英尺(ft)=0.3048米(m)
1磅(lb)=0.454千克(kg)
通過實驗得到撞破腦殼所需要的機械能是mgh=(30*0.454)*9.8*(20*0.3048)=81
 原汁原味的內容在這裡
原汁原味的內容在這裡


【38】一天,harlan的店裡來了一位顧客,挑了25元的貨,顧客拿出100元,harlan沒零錢找不開,就到隔壁飛白的店裡把這100元換成零錢,回來給顧客找了75元零錢。過一會,飛白來找harlan,說剛才的是假錢,harlan馬上給飛白換了張真錢,問harlan賠了多少錢?
A:
100元(貨25元+找給顧客75元=100元)
【39】猴子爬繩這道力學怪題乍看非常簡單,可是據說它卻使劉易斯.卡羅爾感到困惑。至於這道怪題是否由這位因《愛麗絲漫遊奇境記》而聞名的牛津大學數學專家提出來的,那就不清楚了。總之,在一個不走運的時刻,他就下述問題徵詢人們的意見:一根繩子穿過無摩擦力的滑輪,在其一端懸掛著一隻10磅重的砝碼,繩子的另一端有隻猴子,同砝碼正好取得平衡。當猴子開始向上爬時,砝碼將如何動作呢?"真奇怪,"卡羅爾寫道,"許多優秀的數學家給出了截然不同的答案。普賴斯認為砝碼將向上升,而且速度越來越快。克利夫頓(還有哈考特)則認為,砝碼將以與猴子一樣的速度向上升起,然而桑普
森卻說,砝碼將會向下降!"一位傑出的機械工程師說"這不會比蒼蠅在繩子上爬更起作用",而一位科學家卻認為"砝碼的上升或下降將取決於猴子吃蘋果速度的倒數",然而還得從中求出猴子尾巴的平方根。嚴肅地說,這道題目非常有趣,值得認真推敲。它很能說明趣題與力學問題之間的緊密聯絡。
A:
砝碼將以與猴子相同的速度上升,因為它們質量相同,受力也相同。
【40】兩個空心球,大小及重量相同,但材料不同。一個是金,一個是鉛。空心球表面圖有相同顏色的油漆。現在
要求在不破壞表面油漆的條件下用簡易方法指出哪個是金的,哪個是鉛的。
A:
旋轉看速度,金的密度大,質量相同,所以金球的實際體積較小,因為外半徑相同,所以金球的內半徑較大,所以金球的轉動慣量大,在相同的外加力矩之下,金球的角加速度較小,所以轉得慢。
【41】有23枚硬幣在桌上,10枚正面朝上。假設別人矇住你的眼睛,而你的手又摸不出硬幣的反正面。讓你用最好的方法把這些硬幣分成兩堆,每堆正面朝上的硬幣個數相同。
A:
分成10+13兩堆, 然後翻轉10的那堆
【42】三個村莊A、B、C和三個城鎮A、B、C坐落在如圖所示的環形山內。由於歷史原因,只有同名的村與鎮之間才有來往。為方便交通,他們準備修鐵路。問題是:如何在這個環形山內修三條鐵路連通A村與A鎮, B村與B鎮,C村與C鎮。而這些鐵路相互不能相交。(挖山洞、修立交橋都不算,絕對是平面問題)。想出答案再想想這個題說明什麼問題。
答案如右圖:
【43】屋裡三盞燈泡,屋外三個開關,一個開關僅控制一盞燈,屋外看不到屋裡怎樣只進屋一次,就知道哪個開關控制哪盞燈?四盞呢~
溫度,先開一盞,足夠長時間後關了,開另一盞,進屋看,亮的為後來開的,摸起來熱的為先開的,剩下的一盞也就確定了。
四盞的情況:設四個開關為ABCD,先開AB,足夠長時間後關B開C,然後進屋,又熱又亮為A,只熱不亮為B,只亮不熱為C,不亮不熱為D。
【44】2+7-2+7全部有火柴根組成,移動其中任何一根,答案要求為30
A:
說明:因為書寫問題作如下解釋,2是由橫折橫三根組成,7是由橫折兩根組成
1, 改變賦值號.比如+,-,=
2, 注意質數.
3, 可能把畫面顛倒過來.
4, 然後就可以去考慮更改其他數字更改了
247-217=30
【45】5名海盜搶得了窖藏的100塊金子,並打算瓜分這些戰利品。這是一些講民主的海盜(當然是他們自己特有的民主),他們的習慣是按下面的方式進行分配:最厲害的一名海盜提出分配方案,然後所有的海盜(包括提出方案者本人)就此方案進行表決。如果50%或更多的海盜贊同此方案,此方案就獲得通過並據此分配戰利品。否則提出方案的海盜將被扔到海里,然後下一名最厲害的海盜又重複上述過程。所有的海盜都樂於看到他們的一位同夥被扔進海里,不過,如果讓他們選擇的話,他們還是寧可得一筆現金。他們當然也不願意自己被扔到海里。所有的海盜都是有理性的,而且知道其他的海盜也是有理性的。此外,沒有兩名海盜是同等厲害的——這些海盜按照完全由上到下的等級排好了座次,並且每個人都清楚自己和其他所有人的等級。這些金塊不能再分
,也不允許幾名海盜共有金塊,因為任何海盜都不相信他的同夥會遵守關於共享金塊的安排。這是一夥每人都只為自己打算的海盜。最凶的一名海盜應當提出什麼樣的分配方案才能使他獲得最多的金子呢?
如果輪到第四個海盜分配:100,0
輪到第三個:99,0,1
輪到第二個:98,0,1,0
輪到第一個:97,0,1,0,2,這就是第一個海盜的最佳方案。
【46】他們中誰的存活機率最大?
5個囚犯,分別按1-5號在裝有100顆綠豆的麻袋抓綠豆,規定每人至少抓一顆,而抓得最多和最少的人將被處死,而且,他們之間不能交流,但在抓的時候,可以摸出剩下的豆子數。問他們中誰的存活機率最大?
A:
提示:
1,他們都是很聰明的人
2,他們的原則是先求保命,再去多殺人
3,100顆不必都分完
4,若有重複的情況,則也算最大或最小,一併處死
第一個人選擇17時最優的。它有先動優勢。他確實有可能被逼死,後面的2、3、4號也想把1號逼死,但做不到(起碼確定性逼死做不到)
可以看一下,如果第1個人選擇21,他的資訊時暴露給第2個人的,那麼,1號就將自己暴露在一個非常不利的環境下,2-4號就會選擇20,五號就會被迫在1-19中選擇,則1、5號處死。所以1號不會這樣做,會選擇一個更小的數。
1號選擇一個
下面決定的就是1號會選擇一個什麼數,他仍然不會選擇一個太大或太小的數,因為那樣仍然是自己處於不利的地位(2-4號肯定不會留情面的),100/6=16.7(為什麼除以6?因為5號會隨機選擇一個數,對1號來說要儘可能的靠近中央,2-4好也是如此,而且正因為2-4號如此,1號才如此... ...),最終必然是在16、17種選擇的問題。
對16、17進行概率的計算之後,就得出了3個人選擇17,第四個人選擇16時,為均衡的狀態,第4號雖然選擇16不及前三個人選擇17生存的機會大,但是若選擇17則整個遊戲的人必死(包括他自己
)!第3號沒有動力選擇16,因為計算概率可知生存機會不如17。
所以選擇為17、17、17、16、X(1-33隨機),1-3號生存機會最大。
【47】有5只猴子在海邊發現 一堆桃子,決定第二天來平分.第二天清晨,第一隻猴子最早來到,它左分右分分不開,就朝海里扔了一隻,恰好可以分成5份,它拿上自己的一份走了.第 2,3,4,5只猴子也遇到同樣的問題,採用了同樣的方法,都是扔掉一隻後,恰好可以分成5份.問這堆桃子至少有多少隻?
A: 這堆桃子至少有3121只。
第一隻猴子扔掉1個,拿走624個,餘2496個;
第二隻猴子扔掉1個,拿走499個,餘1996個;
第三隻猴子扔掉1個,拿走399個,餘1596個;
第四隻猴
子扔掉1個,拿走319個,餘1276個;
第五隻猴子扔掉1個,拿走255個,餘4堆,每堆255個。
如果不考慮正負,-4為一解
考慮到要5個猴子分,假設分n次。
則題目的解: 5^n-4
本題為5^5-4=3121.
設共a個桃,剩下b個桃,則b=(4/5)((4/5)((4/5)((4/5)((4/5)(a-1)-1)-1)-1)-1)-1),即b=(1024a-8404)/3125 ; a=3b+8+53*(b+4)/1024,而53跟1024不可約,則令b=1020可有最小解,得a=3121 ,設桃數x,得方程
4/5{4/5{4/5[4/5(x-1)-1]-1}-1}=5n
展開得
256x=3125n+2101
故x=(3125n+2101)/256=12n+8+53*(n+1)/256
因為53與256不可約,所以判斷n=255有一解.x為整數,等於3121
【48】話說某天一艘海盜船被天下砸下來的一頭牛給擊中了,5個倒黴的傢伙只好逃難到一個孤島,發現島上孤零零的,幸好有有棵椰子樹,還有一隻猴子!大家把椰子全部採摘下來放在一起,但是天已經很晚了,所以就睡覺先.
晚上某個傢伙悄悄的起床,悄悄的將椰子分成5份,結果發現多一個椰子,順手就給了幸運的猴子,然後又悄悄的藏了一份,然後把剩下的椰子混在一起放回原處,最後還是悄悄滴回去睡覺了.
過了會兒,另一個傢伙也悄悄的起床,悄悄的將剩下的椰子分成5份,結果發現多一個椰子,順手就又給了幸運的猴子,然後又悄悄滴藏了一份,把剩下的椰子混在一起放回原處,最後還是悄悄滴回去睡覺了.
又過了一會 ......
又過了一會 ...
總之5個傢伙都起床過,都做了一樣的事情。早上大家都起床,各自心懷鬼胎的分椰子了,這個猴子還真不是一般的幸運,因為這次把椰子分成5分後居然還是多一個椰子,只好又給它了.問題來了,這堆椰子最少有多少個?
A: 這堆椰子最少有15621
第一個人給了猴子1個,藏了3124個,還剩12496個;
第二個人給了猴子1個,藏了2499個,還剩9996個;
第三個人給了猴子1個,藏了1999個,還剩7996個;
第四個人給了猴子1個,藏了1599個,還剩6396個;
第五個人給了猴子1個,藏了1279個,還剩5116個;
最後大家一起分成5份,每份
1023個,多1個,給了猴子。
【49】小明和小強都是張老師的學生,張老師的生日是M月N日,2人都知道張老師的生日是下列10組中的一天,張老師把M值告訴了小明,把N值告訴了小強,張老師問他們知道他的生日是那一天嗎?
3月4日 /3月5日/ 3月8日 / 6月4日 /6月7日/9月1日 /9月5日
12月1日/ 12月2日/ 12月8日
M小明說:如果我不知道的話,小強肯定也不知道
N小強說:本來我也不知道,但是現在我知道了
小明說:哦,那我也知道了
請根據以上對話推斷出張老師的生日是哪一天
A: 9.1
【50】一邏輯學家誤入某部落,被囚於牢獄,酋長欲意放行,他對邏輯學家說:“今有兩門,一為自由,一為死亡,你可任意開啟一門。
現從兩個戰士中選擇一人負責解答你所提的任何一個問 題(Y/N),其中A一個天性誠實,B一人說謊成性,今後生死任你選擇。”邏輯學家沉思片刻,即向一戰士發問,然後開門從容離去。
A: (問A自由門在那裡或問B死亡之門在那裡)
邏輯學家應如何發問?
問:如果我問另一個人死亡之門在哪裡,他會怎麼回答?
最終得到的回答肯定是指向自由之門的。
【51】說從前啊,有一個富 人,他有30個孩子,其中15個是已故的前妻所生,其餘15個是繼室所生,這後一個婦人很想讓她自己所生的最年長的兒子繼承財產,於是,有一天,他就向他 說:"親愛的丈夫啊,你就要老了,我們應該定下來誰將是你的繼承人,讓我們把我們的30個孩子排成一個圓圈,從他們中的一個數起,每逢到10就讓那個孩子 站出去,直到最後剩下哪個孩子,哪個孩子就繼承你的財產吧!"富人一想,我靠,這個題意相當有內涵了,不錯,彷彿很公平,就這麼辦吧~不過,當剔選過程不 斷進行下去的時候,這個富人傻眼了,他發現前14個被剔除的孩子都是前妻生的,而且下一個要被剔除的還是前妻生的,富人馬上大手一揮,停,現在從這個孩子 倒回去數, 繼室,就是這個歹毒的後媽一想,倒數就倒數,我15個兒子還鬥不過你一個啊~她立即同意了富人的動議,你猜,到底誰做了繼承人呢~
A: 老婆的兒子
【52】“有一牧場,已知養牛27頭,6天把草吃盡;養牛23頭,9天把草吃盡。如果養牛21頭,那麼幾天能把牧場上的草吃盡呢?並且牧場上的草是不斷生長的。”
A:
設牛每天吃掉x,草每天長出y,原來有牧場的草量是a
a=(27x-y)*6=(23x-y)*9
可解出y=15x, a=72x,所以a=(21x-y)*Z
72x=(21x-y)*Z ==> 72x=(21x-15x)*Z==>72X=6X*Z
Z=12 ,所以需要12天。
【53】一個商人騎一頭驢要穿越1000公里長的沙漠,去賣3000根胡蘿蔔。已知驢一次性可馱1000根胡蘿蔔,但每走一公里又要吃掉一根胡蘿蔔。問:商人共可賣出多少胡蘿蔔?
A:
商人帶驢馱1000根胡蘿蔔,先走250公里,這時,驢已吃250根,放下500根,原地返回,又吃掉250根。商人再帶驢馱1000根胡蘿蔔,走到250公里處,這時,驢已吃250根,再馱上原先放的500根中的250根,繼續前行至500公里處,這時,驢又吃250根,放下500根,剩250根返回250公里處,在馱上250公里處剩下的250根返回原地,這時驢又吃250根。
商人再帶驢馱1000根胡蘿蔔,走到500公里處,這時,驢已吃500根,再馱上原先放的500根,走出沙漠,驢吃掉500根,還剩500根。
【54】10箱黃金,每箱100塊,每塊一兩。有貪官,把某一箱的每塊都磨去一錢。請稱一次找到不足量的那個箱子
A:
第一箱子拿1塊,第二箱子拿2塊, 第10箱子拿10塊,然後放在一起稱,看看缺了幾錢,缺了n錢就說明是第n個箱子
【55】你讓工人為你工作7天,給工人的回報是一根金條。金條平分成相連的7段,你必須在每天結束時都付費,如果只許你兩次把金條弄斷,你如何給你的工人付費?
A:
把金條分成1,2,4三段。第一天1,第二天2,第三天1+2……第七天1+2+4。
【56】有十瓶藥,每瓶裡都裝有100片藥(彷彿現在裝一百片的少了,都是十片二十片的,不管,咱們就這麼來了),其中有八瓶裡的藥每片重10克,另有兩瓶裡的藥每片重9克。用一個蠻精確的小秤,只稱一次,如何找出份量較輕的那兩個藥瓶?
等同54,但此題有一些變化,與眾不同的瓶子有兩個,只稱一次的話,只能得到兩個瓶子所缺的克數的總和,我們必須保證能從總和中唯一地得出兩個瓶子的所缺數。第一個瓶可拿出1片,第二個拿2片,第三個拿3片,但第四個不能拿4片,因為如果結果缺了5克的話,你就不知道是缺了2+3還是1+4。所以第四個應拿5片,第五個應拿8片,第n個應拿a(n-1)+a(n-2)片。
【57】一個經理有三個女兒, 三個女兒的年齡加起來等於13,三個女兒的年齡乘起來等於經理自己的年齡,有一個下屬已知道經理的年齡,但仍不能確定經理三個女兒的年齡,這時經理說只有,一個女兒的頭髮是黑的,然後這個下屬就知道了經理三個女兒的年齡。請問三個女兒的年齡分別是多少?為什麼?
A:
顯然3個女兒的年齡都不為0,要不爸爸就為0歲了,因此女兒的年齡都大於等於1歲。這樣可以得下面的情況:1*1*11=11,1*2**10=20,1*3*9=27,1*4*8=32,1*5*7=35,{1*6*6=36},{2*2*9=36},2*3*8=48,2*4*7=56,2*5*6=60,3*3*7=63,3*4*6=72,3*5*5=75,4*4*5=80因為下屬已知道經理的年齡,但仍不能確定經理三個女兒的年齡,說明經理是36歲(因為{1*6*6=36},{2*2*9=36}),所以3個女兒的年齡只有2種情況,經理又說只有一個女兒的頭髮是黑的,說明只有一個女兒是比較大的,其他的都比較小,頭髮還沒有長成
黑色的,所以3個女兒的年齡分別為2,2,9!
【58】有三個人去住旅館,住 三間房,每一間房?元,於是他們一共付給老闆?,第二天,老闆覺得三間房只需要?元就夠了於是叫小弟退回?給三位客人,誰知小弟貪心,只退 回每人?,自己偷偷拿了ū,這樣一來便等於那三位客人每人各花了九元,於是三個人一共花了?,再加上小弟獨吞了不ū,總共是?。可是當初他 們三個人一共付出?那麼還有?呢?
應該是三個人付了9*3=27,其中2付給了小弟,25付給了老闆
【59】有兩位盲人,他們都各自買了兩對黑襪和兩對白襪,八對襪了的布質、大小完全相同,而每對襪了都有一張商標紙連著。兩位盲人不小心將八對襪了混在一起。他們每人怎樣才能取回黑襪和白襪各兩對呢?
A:
拆開所有的襪子,每人一個
【60】有一輛火車
以每小時 15公里的速度離開洛杉磯直奔紐約,另一輛火車以每小時20公里的速度從紐約開往洛杉磯。如果有一隻鳥,以30公里每小時的速度和兩輛火車同時啟動,從洛杉磯出發,碰到另一輛車後返回,依次在兩輛火車來回飛行,直到兩輛火車相遇,請問,這隻小鳥飛行了多長距離?
設總距離為d,總共用時d/(15+20),兩車相遇,所以鳥飛了30*d/(15+20)=6d/7
【61】你有兩個罐子,每個罐子各有若干紅色彈球和藍色彈球,兩個罐子共有50個紅色彈球,50個藍色彈球,隨機選出一個罐子,隨機從中選取出一個彈球,要使取出的是紅球的概率最大,一開始兩個罐子應放幾個紅球,幾個藍球?在你的計劃中,得到紅球的準確機率是多少?
一個罐子放1紅,一個罐子放49紅和50藍,這樣得到紅球的概率接近3/4。
【62】你有四個裝藥丸的罐子,每個藥丸都有一定的重量,被汙染的藥丸是沒被汙染的重量+1.只稱量一次,如何判斷哪個罐子的藥被汙染了?
與前面的54,56題相似。
【63】對一批編號為1~100,全部開關朝上(開)的燈進行以下操作:凡是1的倍數反方向撥一次開關;2的倍數反方向又撥一次開關;3的倍數反方向又撥一次開關……問:最後為關熄狀態的燈的編號。
A:
1 4 9
【64】想象你在鏡子前,請問,為什麼鏡子中的影像可以顛倒左右,卻不能顛倒上下?
A:
實際上鏡子並沒有顛倒左右,而是顛倒前後。
【65】一群人開舞會,每人頭 上都戴著一頂帽子。帽子只有黑白兩種,黑的至少有一頂。每個人都能看到其它人帽子的顏色,卻看不到自己的。主持人先讓大家看看別人頭上戴的是什么帽子,然 後關燈,如果有人認為自己戴的是黑帽子,就打自己一個耳光。第一次關燈,沒有聲音。於是再開燈,大家再看一遍,關燈時仍然鴉雀無聲。一直到第三次關燈,才 有劈劈啪啪打耳光的聲音響起。問有多少人戴著黑帽子?
3 。如果只有1人戴黑帽子,那麼第一次關燈他就會打自己耳光;如果有2人,第二次關燈他們就會打自己耳光;有n人戴帽子的話第n次關燈他們就會打自己耳光。
【66】兩個圓環,半徑分別是1和2,小圓在大圓內部繞大圓圓周一週,問小圓自身轉了幾周?如果在大圓的外部,小圓自身轉幾周呢?
把大圓剪斷拉直。小圓繞大圓圓周一週,就變成從直線的一頭滾至另一頭。因為直線長就是大圓的周長,是小圓周長的2倍,所以小圓要滾動2圈。
但是現在小圓不是沿直線而是沿大圓滾動,小圓因此還同時作自轉,當小圓沿大圓滾動1週迴到原出發點時,小圓同時自轉1周。當小圓在大圓內部滾動時自轉的方向與滾動的轉向相反,所以小圓自身轉了
1周。當小圓在大圓外部滾動時自轉的方向與滾動的轉向相同,所以小圓自身轉了3周。
這一題非常有迷惑性,小圓在外部時其實是3圈,你可以拿個硬幣試試可以把圓看成一根繩子,長繩是短繩的2倍長,假設長繩開始介面在最底下,短繩介面在長繩介面處,然後短繩開始順時針繞,當短繩介面對著正左時,這時其實才繞了長繩的1/4,轉了180+90度,所以繞一圈是270*4=360*3 。同理小圓在內部時是1圈。也可以套用下列公式: 兩圓圓心距/轉動者半徑=轉動者切另一圓時的自轉數!!
【67】 1元錢一瓶汽水,喝完後兩個空瓶換一瓶汽水,問:你有20元錢,最多可以喝到幾瓶汽水?
A:
40瓶,
20+10+5+2+1+1=39, 這時還有一個空瓶子,先向店主借一個空瓶,換來一瓶汽水喝完後把空瓶還給店主。
【68】有3頂紅帽子,4頂黑 帽子,5頂白帽子。讓10個人從矮到高站成一隊,給他們每個人頭上戴一頂帽子。每個人都看不見自己戴的帽子的顏色,卻只能看見站在前面那些人的帽子顏色。 (所以最後一個人可以看見前面9個人頭上帽子的顏色,而最前面那個人誰的帽子都看不見。現在從最後那個人開始,問他是不是知道自己戴的帽子顏色,如果他回 答說不知道,就繼續問他前面那個人。假設最前面那個人一定會知道自己戴的是黑帽子。為什麼?
“有3頂黑帽子,2頂白帽子。讓三個人從前到後站成一排,給他們每個人頭上戴一頂帽子。每個人都看不見自己戴的帽子的顏色,卻只能看見站在前面那些人的帽子顏色。(所以最後一個人可以看見前面兩個人頭上帽子的顏色,中間那個人看得見前面那個人的帽子顏色但看不見在他後面那個人的帽子顏色,而最前面那個人誰的帽子都看不見。現
在從最後那個人開始,問他是不是知道自己戴的帽子顏色,如果他回答說不知道,就繼續問他前面那個人。事實上他們三個戴的都是黑帽子,那麼最前面那個人一定會知道自己戴的是黑帽子。為什麼?”
答案是,最前面的那個人聽見後面兩個人都說了“不知道”,他假設自己戴的是白帽子,於是中間那個人就看見他戴的白帽子。那麼中間那個人會作如下推理:“假設我戴了白帽子,那麼最後那個人就會看見前面兩頂白帽子,但總共只有兩頂白帽子,他就應該明白他自己戴的是黑帽子,現在他說不知道,就說明我戴了白帽子這個假定是錯的,所以我戴了黑帽子。”問題是中間那人也說不知道,所以最前面那個人知道自己戴白帽子的假定是錯的,所以他推斷出自己戴了黑帽子。
我們把這個問題推廣成如下的形式:
“有若干種顏色的帽子,每種若干頂。假設有若干個人從
前到後站成一排,給他們每個人頭上戴一頂帽子。每個人都看不見自己戴的帽子的顏色,而且每個人都看得見在他前面所有人頭上帽子的顏色,卻看不見在他後面任何人頭上帽子的顏色。現在從最後那個人開始,
問他是不是知道自己戴的帽子顏色,如果他回答說不知道,就繼續問他前面那個人。一直往前問,那麼一定有一個人知道自己所戴的帽子顏色。”
當然要假設一些條件:
1)首先,帽子的總數一定要大於人數,否則帽子都不夠戴。
2)“有若干種顏色的帽子,每種若干頂,有若干人”這個資訊是佇列中所有人都事先知道的,而且所有人都知道所有人都知道此事,所有人都知道所有人都知道所有人都知道此事,等等等等。但在這個條件中的“若干”不一定非要具體一一給出數字來。
這個資訊具體地可以是象上面經典的形式,列舉出每種顏色帽子的數目“有3頂黑帽子,2頂白帽子,3個人”,也可以是“有紅黃綠三種顏色的帽子各1頂2頂3頂,但具體不知道哪種顏色是幾頂,有6個人”,甚至連具體人數也可以不知道,“有不知多少人排成一排,有黑白兩種帽子,每種帽子的數目都比人數少1”,這時候那個排在最後的人並不知道自己排在最後——直到開始問他時發現在他回答前沒有別人被問到,他才知道他在最後。在這個帖子接下去的部分當我出題的時候我將只寫出“有若干種顏色的帽子,每種若干頂,有若干人”這個預設條件,因為這部分確定了,題目也就確定了。
3)剩下的沒有戴在大家頭上的帽子當然都被藏起來了,隊伍裡的人誰都不知道都剩下些什麼帽子。
4)所有人都不是色盲,不但不是,而
且只要兩種顏色不同,他們就能分別出來。當然他們的視力也很好,能看到前方任意遠的地方。他們極其聰明,邏輯推理是極好的。總而言之,只要理論上根據邏輯推導得出來,他們就一定推導得出來。相反地如果他們推不出自己頭上帽子的顏色,任何人都不會試圖去猜或者作弊偷看——不知為不知。
5)後面的人不能和前面的人說悄悄話或者打暗號。
當然,不是所有的預設條件都能給出一個合理的題目。比如有99頂黑帽子,99頂白帽子,2個人,無論怎麼戴,都不可能有人知道自己頭上帽子的顏色。另外,只要不是隻有一種顏色的帽子,在只由一個人組成的隊伍裡,這個人也是不可能說出自己帽子的顏色的。
但是下面這幾題是合理的題目:
1)3頂紅帽子,4頂黑帽子,5頂白帽子,10個人。
2)3頂紅帽子,4頂黑帽子,5頂白帽子,8個人。
3)n頂黑帽子,n-1頂白帽子,n個人(n>0)。
4)1頂顏色1的帽子,2頂顏色2的帽子,…
…,99頂顏色99的帽子,100頂顏色100的帽子,共5000個人。
5)有紅黃綠三種顏色的帽子各1頂2頂3頂,但具體不知道哪種顏色是幾頂,有6個人。
6)有不知多少人(至少兩人)排成一排,有黑白兩種帽子,每種帽子的數目都比人數少1。
大家可以先不看我下面的分析,試著做做這幾題。
如果按照上面3頂黑帽2頂白帽時的推理方法去做,那麼10個人就可以把我們累死,別說5000個人了。但是3)中的n是個抽象的數,考慮一下怎麼解決這個問題,對解決一般的問題大有好處。
假設現在n個人都已經戴好了帽子,問排在最後的那一個人他頭上的帽子是什麼顏色,什麼時候他會回答“知道”?很顯然,只有在他看見前面n-1個人都戴著白帽時才可能,因為這時所有的n-1頂白帽都已用光,在他自己的腦袋上只能頂著黑帽子,只要前面有一頂黑帽子,那麼他就無法排除自己頭上是黑帽子的可能——即使他看見前面所有人都是黑帽,他還是有可能戴著第n頂黑帽。
現在假設最後那個人的回答是“不知道”,那麼輪到問倒數第二人。根據最後面那位的回答,他能推斷出什麼呢?如果他看見的都是白帽,那麼他立刻可以推斷出自己戴的是黑帽——要是他也戴著白帽,那麼最後那人應該看見一片白帽,問到他時他就該回答“知道”了。但是如果倒數第二人看見前面至少有一頂黑帽,他就無法作出判斷——他有可能戴著白帽,但是他前面的那些黑帽使得最後那人無法回答“知道”;他自然也有可能戴著黑帽。
這樣的推理可以繼續下去,但是我們已經看出了苗頭。最後那個人可
以回答“知道”當且僅當他看見的全是白帽,所以他回答“不知道”當且僅當他至少看見了一頂黑帽。這就是所有帽子顏色問題的關鍵!
如果最後一個人回答“不知道”,那麼他至少看見了一頂黑帽,所以如果倒數第二人看見的都是白帽,那麼最後那個人看見的至少一頂黑帽在哪裡呢?不會在別處,只能在倒數第二人自己的頭上。這樣的推理繼續下去,對於佇列中的每一個人來說就成了:
“在我後面的所有人都看見了至少一頂黑帽,否則的話他們就會按照相同的判斷斷定自己戴的是黑帽,所以如果我看見前面的人戴的全是白帽的話,我頭上一定戴著我身後那個人看見的那頂黑帽。”
我們知道最前面的那個人什麼帽子都看不見,就不用說看見黑帽了,所以如果他身後的所有人都回答說“不知道”,那麼按照上面的推理,他可以確定自己戴的是黑帽,因為他身後的人必定看見了一頂黑帽——只能是第一個人他自己頭上的那頂。事實上很明顯,第一個說
出自己頭上是什麼顏色帽子的那個人,就是從隊首數起的第一個戴黑帽子的人,也就是那個從隊尾數起第一個看見前面所有人都戴白帽子的人。
這樣的推理也許讓人覺得有點迴圈論證的味道,因為上面那段推理中包含了“如果別人也使用相同的推理”這樣的意思,在邏輯上這樣的自指式命題有點危險。但是其實這裡沒有迴圈論證,這是類似數學歸納法的推理,每個人的推理都建立在他後面那些人的推理上,而對於最後一個人來說,他的身後沒有人,所以他的推理不依賴於其他人的推理就可以成立,是歸納中的第一個推理。稍微思考一下,我們就可以把上面的論證改得適合於任何多種顏色的推論:
“如果我們可以從假設斷定某種顏色的帽子一定會在佇列中出現,從隊尾數起第一個看不見這種顏色的帽子的人就立刻可以根據和此論證相同的論證來作出判斷,他戴的是這種顏色的帽子。現在所有我身後的人都回答不知道,所以我身後的人也看見了此種顏色的帽子。如果在我前面我見不到此顏色的帽子,那麼一定是我戴著這種顏色的帽子。”
當然第一個人的初始推理相當簡單:“佇列中一定有人戴這種顏色的帽子,現在我看不見前面有人戴這顏色的帽子,那它只能是戴在我的頭上了。”
對於題1)事情就變得很明顯,3頂紅帽子,4頂黑帽子,5頂白帽子給10個人戴,佇列中每種顏色至少都該有一頂,於是從隊尾數起第一個看不見某種顏色的帽子的人就能夠斷定他自己戴著這種顏色的帽子,通過這點我們也可以看到,最多問
到從隊首數起的第三人時,就應該有人回答“知道”了,因為從隊首數起的第三人最多隻能看見兩頂帽子,所以最多看見兩種顏色,如果他後面的人都回答“不知道”,那麼他前面一定有兩種顏色的帽子,而他頭上戴的一定是他看不見的那種顏色的帽子。
題2)也一樣,3頂紅帽子,4頂黑帽子,5頂白帽子給8個人戴,那麼佇列中一定至少有一頂白帽子,因為其它顏色加起來一共才7頂,所以佇列中一定會有人回答“知道”。
題4)的規模大了一點,但是道理和2)完全一樣。100種顏色的5050頂帽子給5000人戴,前面99種顏色的帽子數量是1+……+99=4950,所以佇列中一定有第100種顏色的帽子(至少有50頂),所以如果自己身後的人都回答“不知道”,那麼那個看不見顏色100帽子的人就可以斷定自己戴著這種顏色的帽子。
至於5)、6)“有紅黃綠三種顏色的帽子各1頂2頂3頂,但具體不知道哪種顏色是幾頂,有6個人”以及“有不知多少人排成一排,有黑白兩種帽子,每種帽子的數目都比人數少1”,原理完全相同,
我就不具體分析了。
最後要指出的一點是,上面我們只是論證了,如果我們可以根據各種顏色帽子的數量和佇列中的人數判斷出在佇列中至少有一頂某種顏色的帽子,那麼一定有一人可以判斷出自己頭上的帽子的顏色。因為如果所有身後的人都回答“不知道”的話,那個從隊尾數起第一個看不見這種顏色的帽子的人就可以判斷自己戴了此顏色的帽子。但是這並不是說在詢問中一定是由他來回答“知道”的,因為還可能有其他的方法來判斷自己頭上帽子的顏色。比如說在題2)中,如果佇列如下:(箭頭表示佇列中人臉朝的方向)
白白黑黑黑黑紅紅紅白→
那麼在隊尾第一人就立刻可以回答他頭上的是白帽,因為他看見了所有的3頂紅帽子和4頂黑帽子,能留給他自己戴的只能是白帽子了
【69】假設排列著100個乒乓球,由兩個人輪流拿球裝入口袋,能拿到第100個乒乓球的人為勝利者。條件是:每次拿球者至少要拿1個,但最多不能超過5個,問:如果你是最先拿球的人,你該拿幾個?以後怎麼拿就能保證你能得到第100個乒乓球?
首先拿4個 別人拿n個你就拿6-n個
【70】盧姆教授說:“有一次 我目擊了兩隻山羊的一場殊死決鬥,結果引出了一個有趣的數學問題。我的一位鄰居有一隻山羊,重54磅,它已有好幾個季度在附近山區稱王稱霸。後來某個好事 之徒引進了一隻新的山羊,比它還要重出3磅。開始時,它們相安無事,彼此和諧相處。可是有一天,較輕的那隻山羊站在陡峭的山
路頂上,向它的競爭對手猛撲過 去,那對手站在土丘上迎接挑戰,而挑戰者顯然擁有居高臨下的優勢。不幸的是,由於猛烈碰撞,兩隻山羊都一命嗚呼了。
現在要講一講本題的奇妙之處。對飼養山羊頗有研究,還寫過書的喬治.阿伯克龍比說道:“通過反覆實驗,我發現,動量相當於一個自20英尺高處墜落下來 的30磅重物的一次撞擊,正好可以打碎山羊的腦殼,致它死命。”如果他說得不錯,那麼這兩隻山羊至少要有多大的逼近速度,才能相互撞破腦殼?你能算出來 嗎?
1英尺(ft)=0.3048米(m)
1磅(lb)=0.454千克(kg)
通過實驗得到撞破腦殼所需要的機械能是mgh=(30*0.454)*9.8*(20*0.3048)=81
我老媽是很沒邏輯的人,所以跟她相處起來還蠻爆笑的,每次問她問題的時候,通常都得不到答案,例如只要每次我問她「這個好吃嗎」,她就會回我「妳可以先吹涼再吃」之類的,完全答非所問 XD,不過她的藝術細胞超強。其實邏輯測驗好像一直都蠻流行的,接下來要讓大家做的測驗題都是網路上很有名的邏輯測驗題,因為很有名所以也許會有大家做過的題目,無論如何一起來試試看吧。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
第一題

6 隻狐狸用 6 分鐘抓了 6 隻雞,如果要在 60 分鐘抓 60 隻雞需要幾隻狐狸?
A. 6 隻
B. 10 隻
C. 60 隻
答案請往下拉
答案是:A. 6 隻。6 隻狐狸在 6 分鐘可以抓 6 隻雞,那麼給牠們 60(6 x 10)分鐘就可以抓 60(6 x 10)隻雞無誤,狐狸數量不需要增加。
第二題

瑪麗的媽媽有四個小孩,老大叫小春,老二叫小夏,老三叫小秋,那麼老四叫什麼?
答案請往下拉
答案是:瑪麗。因為開頭就說是瑪麗的媽媽。
第三題

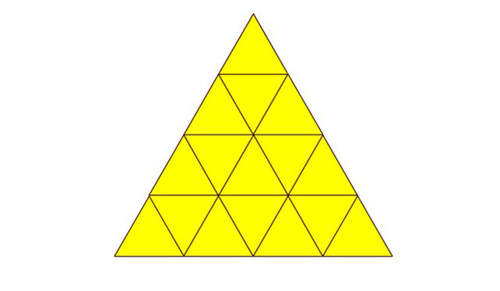
請問上圖有幾個三角形?
答案請往下拉
答案是:27 。總共有四種尺寸的三角形都要記得算進去,最小的小三角形共有 16 個,而由四個小三角形組成的中三角形共有 7 個,由九個小三角形組成的大三角形共有 3 個,最後是不分割的超大三角形 1 個。
第四題

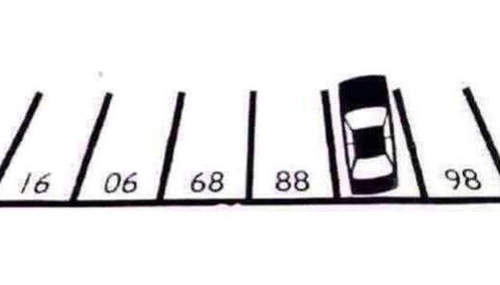
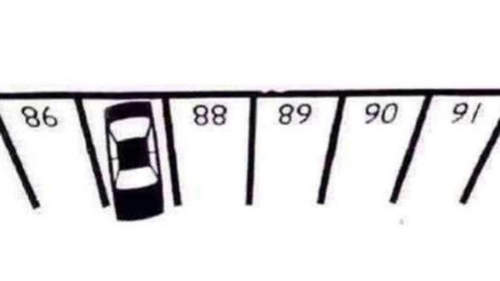
請問這輛車停的停車格是幾號?
A. 76
B. 78
C. 87
D. 97
答案請往下拉
答案是:C. 87。倒過來看就知道了(見下圖)。

第五題

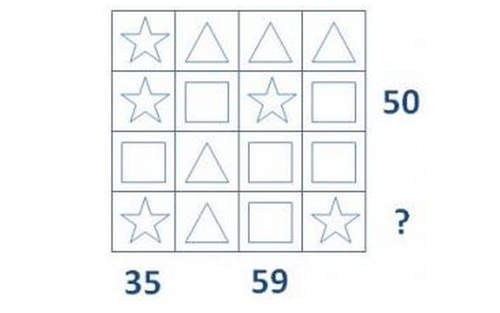
請問在問號的地方應該填上什麼數字?
A. 44
B. 46
C. 52
答案請往下拉
答案是:A. 44。從 35 和 50 的那兩排,可以推測出方塊是 20,星星是 5,接著再把方塊和星星的對應數字帶進 59 那一排,就可推測出三角形是 14,所以問號那一排就是 5 + 14 + 20 + 5 = 44。
最後一題

買一支球棒跟一顆球總共花了 110 元,而球棒比球貴了 100 元,那麼球是多少錢呢?
A. 5 元
B. 10 元
C. 15 元
答案請往下拉
答案是:A. 5 元。球是 5 元,因為球棒比球貴 100 元,所以球棒的價錢是 5 + 100 = 105,所以一支球棒跟一顆球總共要花 5 + 105 = 110 元。


沒有留言:
張貼留言